Chap05 : Mouvements dans un champ uniforme
I - Les forces
1 - Coordonnées d’une force
5.A1 - Représentation des forces
2 - Rappels : poids et champ de pesanteur local
a - Champ de pesanteur
On appelle champ de pesanteur la grandeur vectorielle définie en chaque point de l’espace qui entoure la Terre et qui rend compte de l’attraction que la Terre exerce sur les objets. Il est noté \(\vec{g}\). Son intensité est en \(\pu{N*kg^{–1}}\).
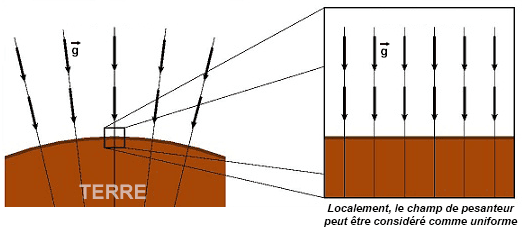
Propriété : Localement, on peut considérer que le champ de pesanteur \(\vec{g}\) est uniforme.
Remarque : A la surface de la Terre, on admet que l’intensité du champ de pesanteur vaut \(g = \pu{9,8 N*kg^{-1}}\).
b - Poids d'un objet
Le poids d'un objet est le nom donné à la force exercée par la Terre (dans son ensemble) sur l’objet du fait de la masse de cet objet. On le note \(\overrightarrow{P_{objet}}\). Son intensité est en \(\pu{N}\).
\(\vec{P}=m·\vec{g}\)
Et donc : \(P = m·g\)
3 - Action du support
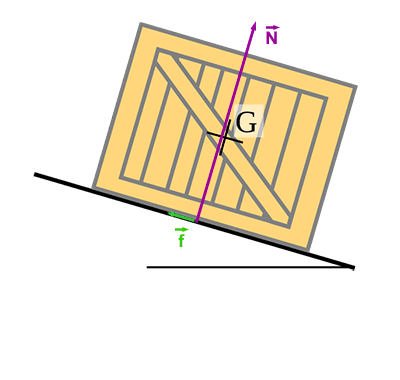
L’action du support sur un objet se décompose en deux forces :
- la normale \(\vec{N}\) : elle existe toujours et est perpendiculaire au support,
- les frottements \(\vec{f}\) :
- ils sont parallèles au support,
- ils sont opposés au sens de déplacement.
Remarque : lorsque les frottements sont négligeables, l’action du support est toujours perpendiculaire au support.
4 - Action d’un fil
La direction de la force exercée par un fil sur un objet est cette du fil.
II - Deuxième loi de Newton
1 - Énoncé
Dans un référentiel galiléen, la somme vectorielle des forces extérieures exercées sur un système ponctuel est égale au produit de la masse de ce système par son vecteur accélération.
\(\sum \overrightarrow{Forces}=m·\overrightarrow{a}\)
2 - Référentiel galiléen
Par définition, un référentiel galiléen est un référentiel dans lequel le principe de l’inertie est respecté.
Tout référentiel en mouvement de translation uniforme par rapport à un référentiel galiléen est lui-même galiléen.
On admet l’existence d’un moins un référentiel galiléen.
3 - Approche qualitative
III - Cas particuliers
1 - Équilibre d’un système
a - Deuxième loi de Newton
Si un système est à l’équilibre alors la somme vectorielle des forces qu’il subit est nulle :
\(\sum \overrightarrow{Forces}=\overrightarrow{0}\)
b - Exemples
5.Eac1 : Caisse immobile sur un plan horizontal 5.Eac2 : Caisse immobile sur un plan incliné
2 - Système animé d’un mouvement rectiligne uniforme
a - Deuxième loi de Newton
Si un système est animé d’un MRU alors la somme vectorielle des forces qu’il subit est nulle :
\(\sum \overrightarrow{Forces}=\overrightarrow{0}\)
b- Exemple
5.Eac3 : Skieur en mouvement rectiligne uniforme
3 - Réciproque
Si un système est tel que \(\sum \overrightarrow{Forces}=\overrightarrow{0}\)
alors son centre de masse est :
- - soit immobile ;
- - soit animé d'un mouvement rectiligne uniforme.
IV - Mouvements dans le champ de pesanteur considéré comme uniforme
1 - Mouvement vertical
5.Eac4 : Exercice du pot de fleur 5.Eac5 : Exercice balle lancée vers le haut
2 - Mouvement parabolique
V - Mouvements dans un champ électrique uniforme
1 - Force électrostatique et champ électrostatique
a - Champ électrostatique
Toute répartition de charges électriques crée dans l’espace qui l’entoure un champ électrique.
Le champ électrostatique est noté \(\overrightarrow{E}\). Son intensité s’exprime en \(\pu{N·C^{–1}}\) ou en \(\pu{V·m^{–1}}\).
b - Force électrostatique
Toute particule de charge \(q\) placée dans un champ électrique \(\overrightarrow{E}\) subit une force électrique : \(\overrightarrow{F_{elec}}=q·\overrightarrow{E}\)
Remarque :
- - si \(q \gt 0\) alors \(\overrightarrow{F_{elec}}\) est dans le même sens que \(\overrightarrow{E}\)
- - si \(q \lt 0\) alors \(\overrightarrow{F_{elec}}\) est opposé à \(\overrightarrow{E}\)
2 - Le condensateur plan
3 - Exemple de mouvement : accélérateur linéaire de particules chargées
VI - Aspect énergétique
5.poly1 - Approche énergétique de la mécanique
1 - Grandeurs
a - Énergie cinétique
L’énergie cinétique d’un système ponctuel de masse \(m\) et de vitesse \(v\) est : \(Ec = \frac{1}{2}·m·v^2\).
b - Énergie potentielle
L’énergie potentiel de pesanteur d’un système de masse \(m\) et d’altitude \(z\) dans un repère d’axe \(Oz\) vertical vers le haut est : \(Epp = m·g·z\).
c - Energie mécanique
L’énergie mécanique d’un système est la somme de son énergie cinétique et de son énergie potentielle de pesanteur : \(Em = Epp + Ec\)
d - Travail d'une force
Le travail d’une force constante \(\vec{F}\) pour un déplacement de sont point d’application de \(A\) à \(B\) est le produit scalaire de la force \(\vec{F}\) par le vecteur déplacement \(\overrightarrow{AB}\).
\(\begin{align} W_{AB}(\vec{F}) &= \vec{F}·\overrightarrow{AB} \\ &= F×AB×cos(\text{angle entre } \overrightarrow{AB} \text{ et } \vec{F}) \end{align}\)
Remarque
Si le travail est positif, le système qui subit la force gagne de l’énergie.
Si le travail est négatif, le système qui subit la force perd de l’énergie.
2 - Lois
a - Conservation de l’énergie mécanique
Remarque : plutôt pour le champ de pesanteur
L’énergie mécanique d’une système soumis uniquement à son poids se conserve.
\(Em = cte\) autrement dit \(Em_A = Em_B\)
b - Théorème de l’énergie cinétique
Remarque : plutôt pour le champ de pesanteur
Dans un référentiel galiléen, au cours d’un déplacement d’un point A à un point B, la variation de l’énergie cinétique d’un système assimilé à un point est égale à la somme des travaux des toutes les forces subies par le système.
\(Ec_B - Ec_A = \sum W_{AB}(\vec{F})\)
