1
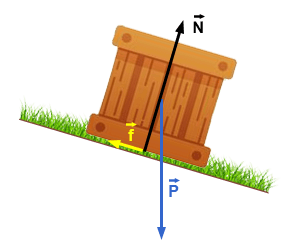
Les forces qui s'exercent sur la caisse sont :
- - son poids \(\vec{P} = m~\vec{g}\)
- - l'action normale du support \(\vec{N}\)
- - les frottement \(\vec{f}\)
2
• Coordonnées des forces
\(\vec{f}
\left|\begin{align}
&f_x = -f \\
&f_y = 0
\end{align}\right.\)
\(\vec{N}
\left|\begin{align}
&N_x = 0 \\
&N_y = N
\end{align}\right.\)
\(\vec{P}
\left|\begin{align}
&P_x = m~g~sin(\alpha) \\
&P_y = -m~g~cos(\alpha)
\end{align}\right.\)
• Deuxième loi de Newton
D'après la deuxième loi de Newton, comme la caisse est immobile : \(\vec{f} + \vec{N} + \vec{P} = \vec{0}\)
• Travail avec les coordonnées
L'expression vectorielle ci-dessus devient :
\(\left\{\begin{align}
&f_x + N_x + P_x = 0 \\
&f_y + N_y + P_y = 0
\end{align}\right.\)
Soit :
\(\left\{\begin{align}
&-f + 0 + m~g~sin(\alpha) = 0 \\
&0 + N - m~g~cos(\alpha) = 0
\end{align}\right.\)
Finalement :
\(\begin{align}
&P = m~g \\
&f = m~g~sin(\alpha) \\
&N = m~g~cos(\alpha)
\end{align}\)