5.A5 : Accélérateur linéaire

Compétences travaillées :

• Exploiter la conservation de l’énergie mécanique ou le théorème de l’énergie cinétique dans le cas du mouvement dans un champ uniforme.

• Discuter de l’influence des grandeurs physiques sur les caractéristiques du champ électrique créé par un condensateur plan, son expression étant donnée.

I - Données physiques

Charge élémentaire : \(e = \pu{1,602E–19 C}\).

Masse de l’électron : \(m = \pu{9,109E–31 kg}\).

Intensité de la pesanteur à la surface de la Terre : \(g = \pu{9,81 N*kg–1}\).

II - Principe de l’accélération d’une particule à l’aide d’un condensateur

On considère un condensateur dont les armatures A et B sont verticales, distante de \(d = \pu{0,50 cm}\) (voir schéma ci-contre). La tension maintenue entre les armatures du condensateur est \(U_{AB} = \pu{25 V}\).

On souhaite étudier le mouvement d’un électron qui entre dans le condensateur au point A avec une vitesse horizontale \(\vec{v_A}\) de valeur \(v_A = \pu{1,5E6 m*s–1}\).

On travaillera dans le repère \((A, x, y)\) représenté sur le schéma. L’origine des temps sera prise lorsque l’électron passe au point \(A\).

1 Coordonnées du vecteur vitesse et du vecteur position de l’électron

Dans cette question, on admettra que le poids de l’électron est négligeable par rapport à la force électrique subie par l’électron.

1.a Donner les caractéristiques (direction, sens et intensité) du champ électrique \(\vec{E}\) qui règne entre les armatures \(A\) et \(B\) du condensateur.

1.b Faire le bilan des forces qui s’exercent sur l’électron.

1.c Donner les caractéristiques (direction, sens et expression littérale de l’intensité) de la force électrique \(\vec{F}\) subie par l’électron.

1.d Exprimer les coordonnées \(F_x\) et \(F_y\) de la force électrique subie par l’électron en fonction de \(e\) et \(E\).

1.e Exprimer les coordonnées \(x_0\) et \(y_0\) du vecteur position à l’instant initial.

1.f Exprimer les coordonnées \({v_0}_x\) et \({v_0}_y\) du vecteur vitesse à l’instant initial.

1.g Énoncer la deuxième loi de Newton.

1.h Appliquer cette loi à l’électron pour en déduire les expressions des coordonnées \(a_x\) et \(a_y\) du vecteur accélération \(\vec{a}\) de l’électron entre l'armature A et l'armature B du condensateur.

1.i En déduire les expressions des coordonnées \(v_x\) et \(v_y\) du vecteur vitesse \(\vec{v}\) de l’électron en fonction du temps.

1.j En déduire les expressions des coordonnées \(x\) et \(y\) de la position de l’électron en fonction du temps.

2 Nature de la trajectoire

Quelle est la nature de la trajectoire de l’électron entre l'armature A et l'armature B du condensateur ? Justifier que l’électron ressort du condensateur par le point \(B\).

3 Cas où \(v_A = 0\)

Dans cette question, on considère que l’électron entre dans le condensateur avec une vitesse \(v_A = 0\).

3.a Exprimer le temps \(t_B\) au bout duquel l’électron parvient au point \(B\) en fonction de \(m\), \(e\), \(d\) et \(E\).

3.b En déduire l’expression de la valeur de la vitesse \(v_B\) de l’électron au point \(B\) en fonction de \(m\), \(e\), \(d\) et \(E\).

3.c Calculer \(v_B\).

3.d Comment doit-on faire varier \(d\) et \(U_{AB}\) pour augmenter la vitesse de l’électron à la sortie de l’accélérateur ?

4 Justification que le poids est négligeable par rapport à la force électrique

4.a Calculer l’intensité de la force électrique subie par l’électron au point \(A\).

4.b Calculer le poids de l’électron.

4.c Que peut-on en conclure ?

III - Principe de l’accélération linéaire de particules

Les accélérateurs linéaires

Les accélérateurs de particules sont utilisés dans plusieurs types de dispositifs.

De petits accélérateurs sont utilisés en médecine, en particulier dans les appareils de radiothérapie.

De grands accélérateurs sont utilisés dans les centres de recherche fondamentale comme au CERN (Centre Européen de Recherche Nucléaire). Le LINAC 4, dernier né des accélérateurs linéaires du CERN, est entré en fonction dans les années 2010. Il permet à des ions hydrogène négatifs H– d’acquérir de très grandes énergies avant d’être envoyés, sous forme de protons, dans un autre accélérateur. Le LINAC 4 mesure 86 mètres de long.

Principe d’un petit accélérateur linéaire

Un accélérateur linéaire est composé des éléments suivants :

- une chambre à vide dans laquelle est maintenu un vide poussé : ce vide permet aux particules accélérées de ne rencontrer aucune autre matière que cette de la cible ;
- une source de particules ;
- une succession de tubes conducteurs reliés à un générateur (un tube sur deux est relié à la même borne) ;

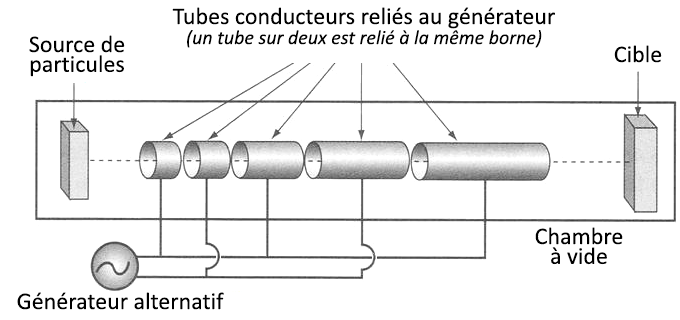
- un générateur de tension alternatif.

Dans chaque tube, le champ électrique est nul car chaque tube porte la même charge.

Entre les tubes, comme deux tubes successifs ont des charges opposées, règne un champ électrique.

Comme le générateur est alternatif, chacune de ses bornes est alternativement positive puis négative (voir schémas de la question 1).

Questions

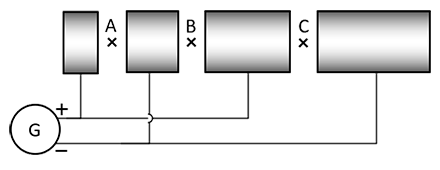
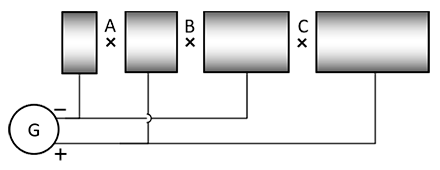
1 Compléter les schémas ci-dessous :

- en indiquant la charge de chaque tube ;
- en représentant le champ électrique aux points A, B, C et D.

2 Sur quelles portions de leur mouvement les particules sont-elles accélérées ?

3 Pourquoi est-il nécessaire que le générateur soit alternatif ?

4 Le rythme du générateur étant régulier, expliquer pourquoi les tubes sont de plus en plus longs.

Afficher la correction

II - Principe de l’accélération d’une particule à l’aide d’un condensateur

1 Coordonnées du vecteur vitesse et du vecteur position de l’électron

1.a

Le champ \(\vec{E}\) est perpendiculaire aux armatures, orienté de l’armature positive A vers l’armature négative B.

Son intensité est : \(\begin{aligned}[t] E &= \dfrac{U_{AB}}{d} \\ &= \dfrac{\pu{25 V}}{\pu{0,0050 m}} \\ &= \pu{5,0E3 V*m–1} \end{aligned}\)

1.b

La seule force qui s’exerce sur l’électron est la force électrique (car le poids de l'électron est négligeable).

1.c

\(\vec{F} = q·\vec{E}\).

Or q < 0.

Donc \(\vec{F}\) est perpendiculaire aux plaques, de l’armature A vers l’armature B.

L’expression de l’intensité de \(\vec{F}\) est \(\begin{aligned}[t] F &= |q·\vec{E}| \\ &= e·E \end{aligned}\)

1.d

\(\vec{F}\) est horizontal vers la droite, donc \(\left\{\begin{aligned} &F_x = +F=eE \\ &F_y = 0 \end{aligned}\right.\)

1.e

A l’instant initial, l’électron est en \(A\), c’est-à-dire l’origine du repère.

Donc \(\left\{\begin{aligned} &x_0 = 0 \\ &y_0 = 0 \end{aligned}\right.\)

1.f

A l’instant initial, l’électron a pour vitesse \(\vec{v_A}\).

Or \(\vec{v_A}\) est horizontal vers la droite.

Donc \(\left\{\begin{aligned} &{v_0}_x = {v_A}_x = v_A \\ &{v_0}_y = {v_A}_y = 0 \end{aligned}\right.\)

1.g

Deuxième loi de Newton : \(\sum\overrightarrow{Forces} = m·\overrightarrow{a}\).

1.h

Dans le cas de l’exercice, la deuxième loi de Newton devient : \(\sum\vec{F} = m·\vec{a}\).

Soit \(\vec{a} = \dfrac{\vec{F}}{m}\).

D’où \(\left\{\begin{aligned} &a_x = \dfrac{F_x}{m} = \dfrac{eE}{m} \\ &a_y = \dfrac{F_y}{m} = 0 \end{aligned}\right.\)

1.i

\(\begin{aligned} v_x &= \text{primitive de } a_x \\ &= \dfrac{eE}{m}·t + {v_x}_0 \\ &= \dfrac{eE}{m}·t + v_A \end{aligned}\)

\(\begin{aligned} v_y &= \text{primitive de } a_y \\ &= {v_y}_0 \\ &= 0 \end{aligned}\)

1.j

\(\begin{aligned} x &= \text{primitive de } v_x \\ &= \frac{1}{2}·\dfrac{eE}{m}·t^2 + v_a·t + x_0 \\ &= \dfrac{eE}{2m}·t^2 + v_A·t \end{aligned}\)

\(\begin{aligned} y &= \text{primitive de } v_y \\ &= y_0 \\ &= 0 \end{aligned}\)

2 Nature de la trajectoire

D’après les équations horaires, on peut dire que la trajectoire est rectiligne et horizontale (car \(y = 0\)).

Donc, l’électron passe bien par B.

3 Cas où \(v_A = 0\)

Dans cette question on a \(v_A = 0\).

3.a

L’électron est en \(B\) lorsque \(x=d\). Donc à l'instant \(t = t_B\), \(x = d\)

Soit \(d = \dfrac{eE}{2m}·{t_B}^2 + v_A·t_B\), avec \(v_A = 0\).

D’où \(d = \dfrac{eE}{2m}·{t_B}^2\).

Soit \(t_B = \sqrt{\dfrac{2md}{eE}}\).

3.b

\(v_B = v(t_B)\).

Or, comme \(v_y = 0\) et \(v_A = 0\), \(v = |v_x| = \dfrac{eE}{m}·t\)

D'où \(\begin{aligned}[t] v_B &= v_x(t_B) \\ & = \dfrac{eE}{m}·t_B \\ &= \dfrac{eE}{m}·\sqrt{\dfrac{2md}{eE}} \\ &= \sqrt{\dfrac{2eEd}{m}} \end{aligned}\)

3.c

\(\begin{aligned}[t] v_B &= \sqrt{\dfrac{2eEd}{m}} \\ &= \sqrt{\dfrac{2 × (\pu{1,6E-19 C}) × (\pu{5,0E3 V*m-1}) × (\pu{0,005 m})}{\pu{9,1E-31 kg}}} \\ &= \pu{3,0E6 m*s-1} \end{aligned}\)

3.d

Comme \(v_B=\sqrt{\dfrac{2eEd}{m}}\) on a aussi \(v_b = \sqrt{\dfrac{2·e·U_{AB}}{m}}\).

Donc pour augmenter \(v_B\), il faut augmenter \(AB\).

Par contre, la modification de \(d\) ne change pas \(v_B\).

4 Justification que le poids est négligeable par rapport à la force électrique

4.a

\(\begin{aligned}[t] F &= eE \\ &= (\pu{1.6E-19 C}) × (\pu{5,0E3 V*m-1}) \\ &= \pu{8,0E-16 N} \end{aligned}\)

4.b

\(\begin{aligned}[t] P &= mg \\ &= (\pu{9,1E-31 C}) × (\pu{9,8 N*kg-1}) \\ &= \pu{8,9E-30 N} \end{aligned}\)

4.c Que peut-on en conclure ?

On peut en conclure que le poids est négligeable par rapport à la force électrique.

III - Principe de l’accélération linéaire de particules

Le champ eléctrique \(\vec{E}\) est représenté en bleu sur les schémas.

Les particules sont accélérées sur toutes les portions entre les tubes (hachures en rouge sur le schéma).

Prenons l’exemple d’une particule positive.

Pour que la particule soit accélérée, il faut qu’elle subisse une force qui soit toujours orientée vers la droite. Il faut donc que le champ \(\vec{E}\) soit toujours vers la droite. Ainsi, quand la particule est en \(A\), il faut la configuration de gauche, quand elle est en \(B\), il faut la configuration de droite, etc. Il faut donc bien que les signes des bornes du générateur changent.

Image animée du principe de l'accélérateur linéaire

Comme la particule va de plus en plus vite, il faut qu’elle parcourt une distance de plus en plus grande pour que le temps mis pour parcourir cette distance soit le même. Ainsi, le temps mis par la particule pour aller de \(A\) à \(B\) est le même que celui pour aller de \(B\) à \(C\), etc. ; et c’est le même que le rythme du générateur.