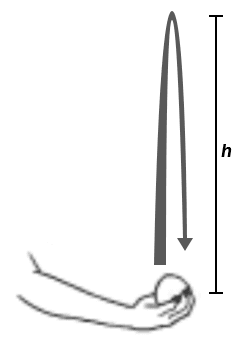
Préambule
Système : la balle
Référentiel d'étude : référentiel terrestre considéré comme galiléen
Bilan des forces : \(\vec{P} = m~\vec{g}\)
Application de la deuxième loi de Newton pour avoir \(\vec{a}\)
Énoncé de la loi : \(\Sigma{\overrightarrow{forces}} = m~\vec{a}\)
Donc ici : \(\vec{P} = m~\vec{a}\)
Soit encore : \(m~\vec{g} = m~\vec{a}\)
Et donc : \(\vec{a} = \vec{g}\)
Choix du repère de travail
Coordonnées du vecteur accélération dans le repère \((O, z)\)
\(\begin{align}
a_z &= g_z \\
&= -g
\end{align}\)
Coordonnées du vecteur vitesse
Les coordonnées du vecteur vitesse sont les primitives des coordonnées du vecteur accélération.
\(\begin{align}
v_z &= \text{primitive de }a_z \\
&= -gt + v_{z_0}
\end{align}\)
Coordonnées du vecteur position
Les coordonnées du vecteur position sont les primitives des coordonnées du vecteur vitesse.
\(\begin{align}
z &= \text{primitive de } v_z \\
&= -\frac{1}{2}gt + v_{z_0}t + z_0
\end{align}\)
Condition utilisations
Les conditions initiales sont donc :
- - pour la position : \(z_0 = 0\)
- - pour la vitesse : \(v_{z_0} = v_0\)
Les équations deviennent donc :
- \(a_z = -g\)
- \(v_z = -gt + v_0\)
- \(z = -\frac{1}{2}gt^2 + v_0t\)
Détermination de h
On note \(t_m\) l'instant au bout duquel la balle atteint sa hauteur maximale.
Lorsque la balle est à sa hauteur maximale, c'est-à-dire pour \(t = t_m\), on a :
- - pour la vitesse : \(v_z(t_m) = 0\)
- - pour l'altitude : \(z(t_m) = h\)
Donc, à partir de la relation pour la vitesse à \(t = t_m\), on obtient :
\(-g~t_m + v_0 = 0\)
Soit \(t_m = \dfrac{v_0}{g}\)
A partir de la relation pour l'altitude à \(t = t_m\) et de l'expression de \(t_m\) trouvée ci-dessous, on obtient :
\(h = -\frac{1}{2}gt_m^2 + v_0t_m\)
Soit : \(h = -\frac{1}{2}g\left(\dfrac{v_0}{g}\right)^2 + v_0\left(\dfrac{v_0}{g}\right)\)
Soit : \(h = -\frac{1}{2}\dfrac{v_0^2}{g} + \dfrac{v_0^2}{g}\)
Soit : \(h = \frac{1}{2}\dfrac{v_0^2}{g}\)
Finalement : \(h = \dfrac{v_0^2}{2~g}\)