Chap16 : Décroissance radioactive
I - Désintégration et diagramme (N,Z)
1) Composition d'un noyaux et isotopes
• Composition d'un noyau
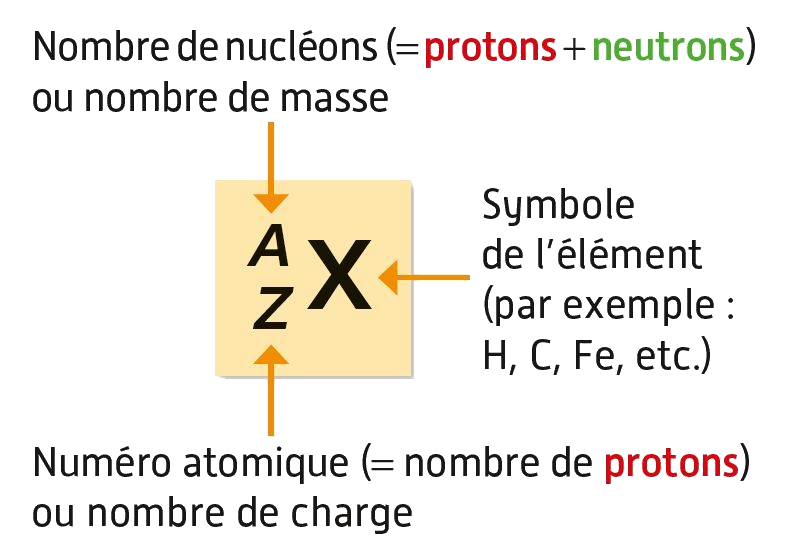
Le noyau de l'atome est constitué de protons et de neutrons :
- • Nombre de proton : numéro atomique Z
- • Nombre de neutrons : N.
- • Nombre de nucléons (protons et neutrons) : nombre de masse A.
• Isotopes
Les atomes d'un même élément chimique ont le même symbole et le même nombre de protons mais peuvent avoir un nombre de neutrons différent, ce sont des isotopes.
2) Diagramme (N,Z) et isotopes
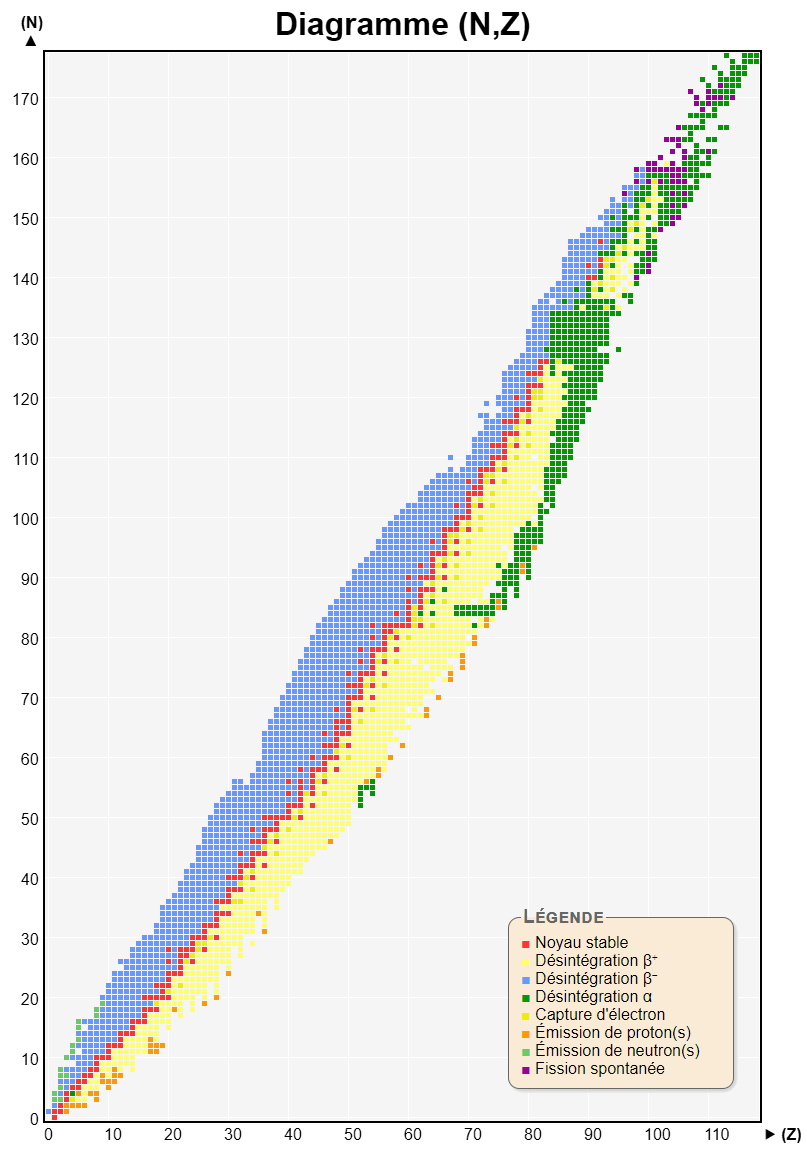
Le diagramme (N, Z) permet de visualiser l'ensemble des noyaux connus.
Lien : Diagramme (N,Z)
Attention : le diagramme (N,Z) peut aussi être représenté avec N en abscisse et Z en ordonnée.
Sur le diagramme (N,Z) ci-contre, les isotopes sont sur une même colonne.
3) Noyaux stables
On recense 279 noyaux stables (en rouge sur le diagramme ci-contre).
Dans le diagramme (N,Z), les noyaux stables constituent ce que l'on appelle la "vallée de stabilité".
Pour Z < 20, les noyaux stables ont un nombre de neutrons N à peu près égal à leur nombre de protons Z.

4) Noyaux instables, radioactifs
La majorité des noyaux sont instables (on dit aussi radioactifs) et se désintègrent.
On distingues différents types de désintégration.
Désintégration β-
Lors d'une désintégration β-, un noyau père forme un noyau fil avec émission d'un électron (\(\ce{^0_-1e}\)).
\(\ce{^A_ZX -> ^A_{Z+1}X + ^0_-1e}\)
Les noyaux émetteurs β– ont un excédant de neutrons par rapport à l'isotope stable.
Désintégration β+
Lors d'une désintégration β+, un noyau père forme un noyau fil avec émission d'un positon (\(\ce{^0_1e}\) ou \(\ce{e^+}\)).
\(\ce{^A_ZX -> ^A_{Z-1}X + ^0_1e}\)
Les noyaux émetteurs β+ ont un déficit de neutrons par rapport à l'isotope stable.
Désintégration α
Lors d'une désintégration α, un noyau père forme un noyau fil avec émission d'une particule &alpha, c'est-à-dire un noyau d'hélium \(\ce{^4_2He}\).
\(\ce{^A_ZX -> ^A_{Z-1}X + ^4_2He}\)
Les noyaux émetteurs α sont principalement des noyaux lourds (Z élevé).
Emission γ
Lors d'une désintégration β− ou β+ (et parfois lors d'une désintégration α), le noyau fils peut se trouver dans un état excité, c'est-à-dire avec un excédant d'énergie, on le note alors \(\ce{Y^*}\).
Le noyau fils excité va se désexciter, c'est-à-dire retourner à son état fondamental, en émettant un rayonnement gamma.
Le rayonnement γ est une onde électromagnétique de très courte longueur d'onde. Il est très pénétrant et dangereux.
\(\ce{^A_ZY^* -> ^A_ZY + γ}\)
5) Chaine de désintégration
Un noyau radioactif peut former un noyau qui est lui même radioactif, et ainsi de suite. On parle de chaine de désintégration.
Un chaine de désintégration finit par la formation d'un noyau stable.
Un chaine de désintégration peut se représenter sur le diagramme (N,Z).
II - Décroissance d'une population de noyaux radioactifs
1) Décroissance exponentielle
Equation différentielle pour \(N(t)\)
Notons \(N(t)\) le nombre de noyaux radioactif dans un échantillon et \(ΔN(t)\) la variation du nombre de noyaux pendant une durée \(Δt\). Remarque : \(ΔN\) est négatif car \(N\) décroit.
On choisi de modéliser l'évolution de \(N(t)\) en affirmant que la variation du nombre de noyaux par unité de temps est proportionnelle au nombre de noyau.
Mathématiquement, cela donne l'équation suivante : \(\frac{ΔN}{Δt} = -λ N\).
Avec \(Δt \to 0\) on obtient : \(\dfrac{dN}{dt} = -λN\) où λ est la constante radioactive du noyau (en \(\pu{s-1}\)).
C'est une équation différentielle pour \(N(t)\).
Solution de l'équation différentielle
La solution de l'équation différentielle précédente est : \(N(t) = N_0·e{-λt}\).

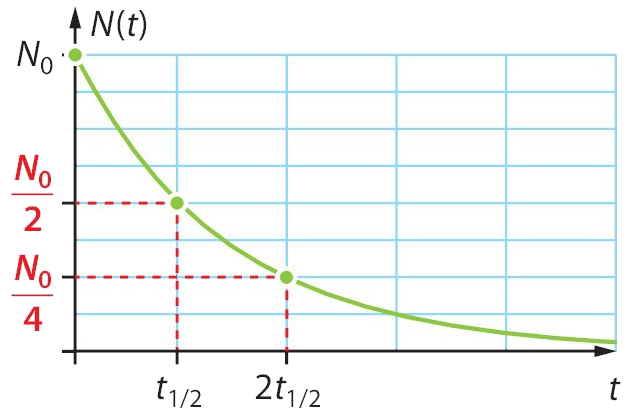
2) Demi-vie
La demi-vie radioactive est le temps au-bout duquel la moitié des noyaux radioactifs initialement présent se sont désintégrés.
On montre que : \(t_{1/2} = \dfrac{ln(2)}{λ}\)
Démonstration :
On a \(N(t_{1/2}) = \frac{N_0}{2}\) et \(N(t_{1/2}) = N_0·e^{-λt_{1/2}}\).
D'où \(\frac{N_0}{2} = N_0·e^{-λt_{1/2}}\)
Soit \(\frac{1}{2} = e^{-λt_{1/2}}\)
Soit \(ln(\frac{1}{2}) = ln(e^{-λt_{1/2}})\)
Soit \(-ln(2) = -λt_{1/2}\)
Finalement : \(t_{1/2} = \dfrac{ln(2)}{λ}\)
3) Activité
L'activité d'un échantillon de noyaux radioactif est le nombre de désintégrations qui se produisent par unité de temps. Elle se note \(A(t)\) et s'exprime en Becquerel (\(\pu{Bq}\)).
\(\pu{1 Bq}\) = 1 désintégrations/s
On montre que : \(A(t) = A_0·e^{-λt}\) et \(A(t) = λ·N(t)\).
Démonstration :
Par définition \(A(t) = \frac{ΔN}{Δt}\).
Soit, avec \(Δt \to 0\), \(A(t) = \dfrac{dN(t)}{dt}\). Donc \(A(t)\) est la dérivé de \(N(t)\).
Donc \(A(t) = λ·N_0·e^{-λt}\).
Donc en prenant \(A_0 = λ·N_0\), on a \(A(t) = A_0·e^{-λt}\)
III - Applications de la radioactivité
1) Principe de la datation
16.A3 : Datation au carbone 14
La connaissance de \(A(t_1)\) et de \(A_0\) permet de déterminer \(t_1\).
Démonstration :
\(A(t_1) = A_0·e^{-λt_1}\)
\(\dfrac{A(t_1)}{A_0} = e^{-λt_1}\)
\(ln(\dfrac{A(t_1)}{A_0}) = ln(e^{-λt_1})\)
\(ln(\dfrac{A(t_1)}{A_0}) = -λt_1\)
\(t_1 = -\frac{1}{λ}·ln(\dfrac{A(t_1)}{A_0})\)
2) Application en médecine
16.A4 : Radioactivité en médecine
