12.E2 : Évolution de la charge électrique

On charge un condensateur de capacité \(\pu{C = 70 nF}\) grâce au montage ci-dessous où le générateur a une force électromotrice \(\pu{E = 6,0 V}\).

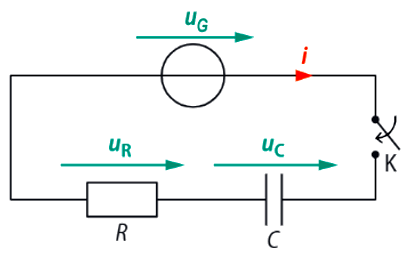
On ferme l’interrupteur K à l’instant \(t = \pu{0 s}\) pris comme origine.

L’allure de la charge \(q\) portée par l’armature positive au cours du temps est donnée par le graphique ci-dessous.

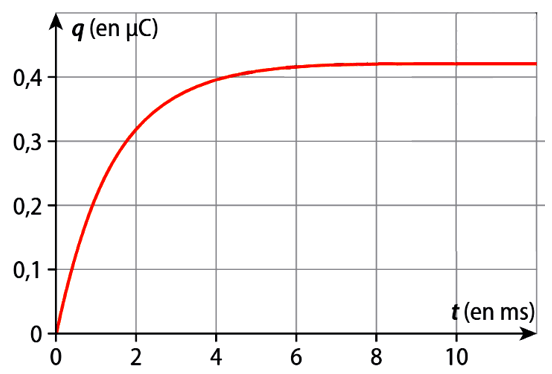
1 Quelle armature porte la charge positive \(q\) ?

2 En utilisant les lois des circuits électriques, montrer que \(q\) vérifie l’équation différentielle suivante : \(\dfrac{dq}{dt}+\dfrac{q}{RC}=\dfrac{E}{R}\)

3 On propose la fonction suivante comme solution de l’équation différentielle : \(q(t)=a + b·exp(-\frac{t}{\tau})\)

3.a Déterminer l’expression de \(a\) pour que cette fonction soit effectivement solution de l’équation.

3.b Que vaut \(q\) à l’instant \(t = 0\) ? En déduire l’expression de \(b\).

3.c Les résultats obtenus sont-ils en accord avec le graphique ?

4 Déterminer la valeur de \(R\).

Afficher la correction

1)

Le courant arrive dans le condensateur par la droite, c'est donc l'armature de droite qui porte la charge positive.

2)

Loi des mailles : \(u_G = u_R + u_C\)

Relation pour le générateur : \(u_G = E\)

Loi pour la résistance : \(u_R = R·i\)

Loi pour le condensateur : \(i = C·\dfrac{du_C}{dt}\)

On sait par ailleurs que \(i=\dfrac{dq}{dt}\) et que \(q = C·u_C\)

Finalement la relation \(u_G = u_R + u_C\) devient : \(E = R·i + \dfrac{q}{C}\)

Soit : \(E = R·\dfrac{dq}{dt} + \dfrac{q}{C}\)

Et donc, en divisant par R : \(\dfrac{E}{R} = \dfrac{dq}{dt} + \dfrac{q}{RC}\)

3.a)

On part de : \(q=a + b·exp(-\frac{t}{\tau})\)

D'où : \(\dfrac{dq}{dt} = 0 + b·\dfrac{-1}{\tau}·exp(-\frac{t}{\tau})\)

En reportant ces deux expressions dans l'équation différentielle on obtient :

\(b·\dfrac{-1}{\tau}·exp(-\frac{t}{\tau})+\dfrac{1}{RC}·\left(a + b·exp(-\frac{t}{\tau})\right) = \dfrac{E}{R}\)

Et donc : \(\left( \dfrac{a}{RC}-\dfrac{E}{R} \right) = \left( \dfrac{-b}{\tau} + \dfrac{b}{RC} \right)·exp(-\frac{t}{\tau})\)

Pour que cette relation soit correcte quelque soit \(t\), il faut que :

- d'une part \(\left( \dfrac{a}{RC}-\dfrac{E}{R} \right)=0\), soit \(a = E·C\)
- d'autre part \(\left( \dfrac{-b}{\tau} + \dfrac{b}{RC} \right) = 0\), soit \(\tau = RC\)

3.b)

A l'instant \(t = \pu{0 s}\), \(q = \pu{0 C}\)

Or \(q(t = 0)=a + b·exp(-\frac{0}{\tau})\). Soit \(q(t = 0)=a + b\)

Donc \(b = -a\).

Soit \(b = -E·C\)

3c)

\(E·C = (\pu{6,0 V})×(\pu{70E-9 F}) = \pu{4,2E-7 C} = \pu{0,42 µC}\)

D'après le graphique, cette valeur correspond bien à la valeur atteinte par \(q\) lorsque les valeurs sont stabilisées.

4)

Graphiquement, on détermine que \(\tau = \pu{1,5 ms}\)

Or \(\tau = RC\)

\(\begin{align} R &= \dfrac{\tau}{C} \\ &= \dfrac{\pu{1,5E-3 s}}{\pu{70E-9 F}} \\ &= \pu{2,0E4 \Omega} \end{align}\)