12.E1 : Décharge d’un condensateur dans une résistance

Un condensateur de capacité \(C\), initialement déchargé, est associé en série avec une résistance.

La tension entre les bornes du condensateur en fonction du temps est enregistrée à l’aide d’un dispositif d’acquisition.

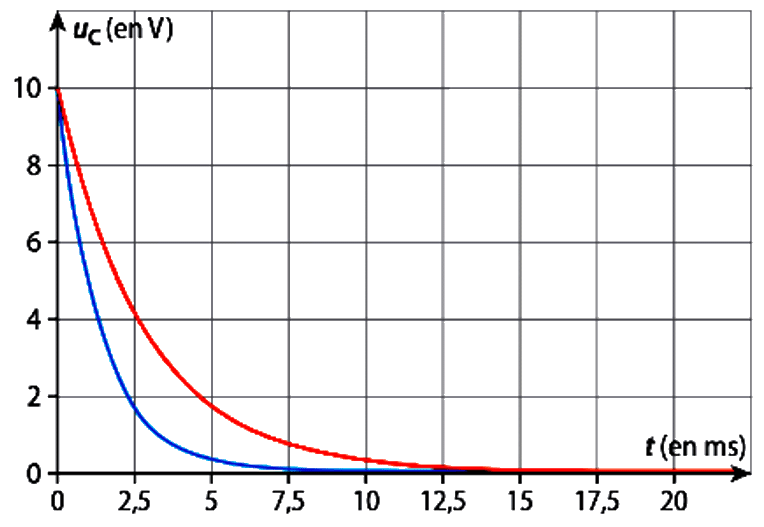
La courbe bleue est obtenue avec une résistance \(R_1 = \pu{20,0 kΩ}\), la courbe rouge avec une résistance \(R_2\) de valeur inconnue.

1 \(R_2\) est-elle supérieure ou inférieure à \(R_1\) ?

2 Déterminer graphiquement le temps caractéristique \(\tau_1\) de la courbe bleue. En déduire la valeur de \(C\).

3 Parmi les valeurs suivantes, déterminer celle de \(R_2\) : \(\pu{12,0 kΩ}\) ; \(\pu{38,0 kΩ}\) ; \(\pu{47,0 kΩ}\) ; \(\pu{68,0 kΩ}\)

Afficher la correction

1)

Le temps caractéristique de la décharge est \(\tau = R·C\).

D'après les courbes, le temps caractéristique de la courbe bleue est plus petit que celui de la courbe rouge.

La valeur de la capacité du condensateur est la même pour les deux courbes.

Donc \(R_1\) (courbe bleue) est inférieure à \(R_2\) (courbe (rouge).

2)

Détermination de \(\tau_1\)

Méthode de la tangente à l'origine

On trace la tangente à l'origine (droite verte)

Méthode du \(\pu{37 \%}\)

(Tracé oragne)

Finalement on trouve \(\tau_1 = \pu{1,5 ms}\)

Détermination de \(C\)

\(\tau_1 = R_1·C\)

\(\begin{align} C &= \dfrac{\tau_1}{R_1} \\ &= \dfrac{\pu{1,5E-3 s}}{\pu{20,0E3 \Omega}} \\ &= \pu{7,5E-8 F} \end{align}\)

3)

Détermination de \(\tau_2\)

Graphiquement, on trouve \(\tau_2 = \pu{3,0 ms}\)

Détermination de \(R_2\)

\(\tau_2 = R_2·C\)

\(\begin{align} R_2 &= \dfrac{\tau_2}{C} \\ &= \dfrac{\pu{3,0E-3 s}}{\pu{7,5E-8 F}} \\ &= \pu{\pu{4,0E4 \Omega}} \end{align}\)

Bilan : La valeur la plus proche est \(R_2 = \pu{38 k\Omega}\)