1
Demi-équation : \(\left(~~\ce{Cu^2+ + 2 e- = {\color{red} Cu} }~~\right)~~×1\)
Demi-équation : \(\left(~~\ce{{\color{red} Ag^+} + e- = Ag}~~\right)~~×2\)
Équation : \(\ce{Cu(s) + 2 Ag+(aq) <--> Cu^2+(aq) + 2 Ag}\)
2
Tableau d'avancement
Détermination de l’avancement maximal :
• Détermination des quantités de matières initiales
\(\begin{align}
n_0(\ce{Cu}) &= \dfrac{m(Cu)}{M(Cu)} \\
&= \dfrac{5,0}{63,5} \\
&= \pu{7,87E–2 mol}
\end{align}\)
\(\begin{align}
n_0(\ce{Ag+}) &= [\ce{Ag+}]·V_{sol~Ag^+} \\
&= 0,075 × 0,100 \\
&= \pu{7,5E–3 mol}
\end{align}\)
• Détermination du réactif en défaut
Faisons l’hypothèse que \(\ce{Ag+}\) est en défaut. Alors \(n_{max}(\ce{Ag+}) = 0\). Soit \(x_{max} = n_0(\ce{Ag+})/2 = \pu{3,75E–3 mol}\).
Faisons l’hypothèse que \(\ce{Cu}\) est en défaut. Alors \(n_{max}(\ce{Cu}) = 0\). Soit \(x_{max} = n_0(\ce{Cu}) = \pu{3,93E–2 mol}\).
Conclusion : le réactif en défaut est \(\ce{Ag+}\) et \(x_{max} = \pu{3,75E–3 mol}\).
Détermination de l’avancement final
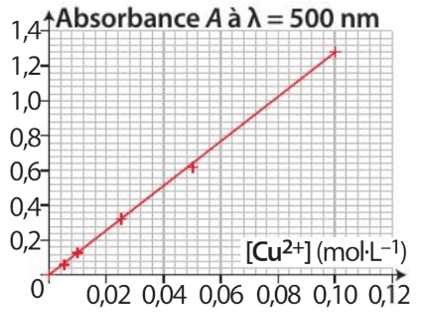
D’après les données, l’absorbance dans l’état finale est \(A_f = \pu{0,47}\).
Or, d’après le graphique, pour cette absorbance \([\ce{Cu^2+}]_f = \pu{0,037 mol*L–1}\).
Or, d’après le tableau d’avancement, \(x_f = n_f(\ce{Cu^2+}) = [\ce{Cu^2+}]_f·V_{final}\). Soit \(x_f = 0,037 × 0,100 = \pu{3,7E–3 mol}\).
Conclusion
On vient de voir que \(x_{max} = \pu{3,75E–3}\) mol et que \(x_f = \pu{3,7E–3 mol}\).
Compte tenu de la précision des mesure sur le graphique, on peut en déduire que \(x_f = x_{max}\).
Donc la réaction est totale