8.Etb2 : Acoustique d'une salle
Dans les salles de spectacle, il existe des places appelées « places aveugles ». Installé à ce type de place, un élève se rend compte que la qualité sonore du concert ne le satisfait pas.
L’objectif de cet exercice est d’étudier la diffraction des ondes lumineuses puis de montrer comment le phénomène de diffraction des ondes sonores permet de retrouver l’emplacement de l’élève dans la salle.
Étude de la diffraction des ondes lumineuses
En rentrant du concert, l’élève consulte une activité expérimentale sur la diffraction des ondes lumineuses dont voici un extrait : « On dispose d’un laser de longueur d’onde inconnue \(\lambda\) face à une fente de largeur a réglable et d’un écran situé à une distance \(D\) égale à \(\pu{2,00 m}\) de la fente. On observe sur l’écran une figure de diffraction de tâche centrale de largeur \(L\). Le schéma de la figure 1 modélise le montage réalisé. »
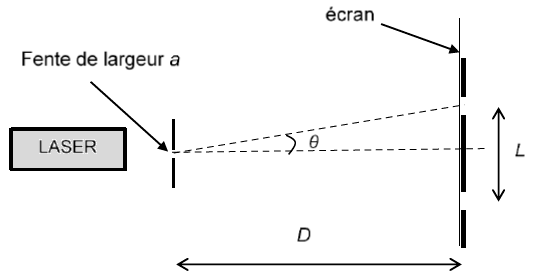
L'angle caractéristique de diffraction \(\theta\), en radian, a pour expression : \(\theta = \dfrac{\lambda}{a}\). L’angle \(\theta\) étant petit, on peut considérer que la valeur de la tangente de l’angle \(\theta\) est égale à l’angle \(\theta\) : \(tan \theta = \theta\).
1 Montrer que la largeur \(L\) de la tâche centrale de diffraction a pour expression : \(L = \dfrac{2\ \lambda\ D}{a}\).
Lors de l’activité expérimentale, des mesures de la largeur \(L\) de la tâche centrale de diffraction sur l’écran ont été effectuées en faisant varier la taille \(a\) de la fente.
L’élève a ensuite obtenu le graphique de la figure 2.
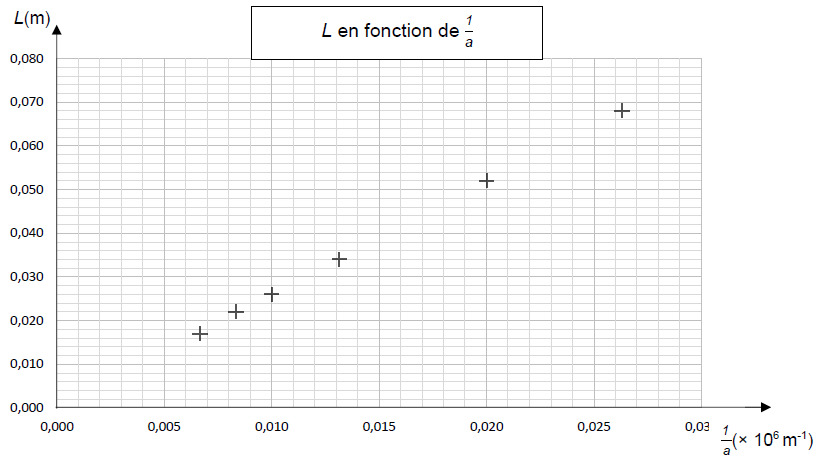
2 À l’aide de la figure 2, montrer que la relation entre \(L\) et \(\dfrac{1}{a}\) est du type \(L = k × \dfrac{1}{a}\).
3 En utilisant la relation donnée question 1. indiquer l’expression de \(k\) en fonction de \(\lambda\) et \(D\).
4 Montrer que la valeur de la longueur d’onde \(\lambda\) est égale à \(\pu{6,5E–7 m}\).
La valeur de l’angle \(\theta_1\) correspondant à la fente de largeur \(a_1 = \pu{38 μm}\) est égale à \(\pu{1,7E–2 rad}\).
5 Déterminer la valeur de l’angle \(\theta_2\) en radian, correspondant à la fente de largeur \(a_2\) égale à \(\pu{150 μm}\).
6 En déduire que la diffraction est la plus marquée pour la fente de largeur \(a_1\).
Étude de la diffraction des ondes sonores
On rappelle que les caractéristiques de diffraction des ondes sont les mêmes pour les ondes lumineuses et les ondes sonores.
Lors du concert, l’élève constate qu’il perçoit mieux les sons graves de fréquence \(f_1\) égale à \(\pu{200 Hz}\) que les sons aigus de fréquence \(f_2\) de valeur \(\pu{1,00 kHz}\).
Donnée : Vitesse du son dans l’air à la température de \(\pu{20 °C}\) : \(V_{son} = \pu{340 m*s–1}\)
7 Exprimer la longueur d’onde \(\lambda\) d’une onde sonore en fonction de la vitesse du son \(V_{son}\) et de sa fréquence \(f\).
8 Montrer que les longueurs d’onde \(\lambda_1\) et \(\lambda_2\) correspondant aux sons de fréquence \(f_1\) et \(f_2\) ont pour valeurs \(\lambda_1 = \pu{1,70 m}\) et \(\lambda_2 = \pu{0,340 m}\).

La figure 3 ci-dessus représente la scène, un pilier de largeur voisine de \(\pu{70 cm}\) et les positions possibles de l’élève lors du concert, repérées par les lettres A, B et C.
On admettra que la diffraction par le pilier est identique à celle créée par une fente de même largeur.
9 En se référant à la figure 1 et à la réponse apportée à la question 8, choisir, en justifiant qualitativement, parmi les positions A, B ou C celle qui correspondrait le mieux à la situation décrite par l’élève lors du concert.
