8.E2 : Onde le long d'une corde

La propagation d’une onde le long de la corde est étudiée par chronophotographie. Quatre images consécutives sont reproduites ci-dessus. L’intervalle de temps séparant deux photos consécutives est \(Δt = \pu{0,25 s}\).

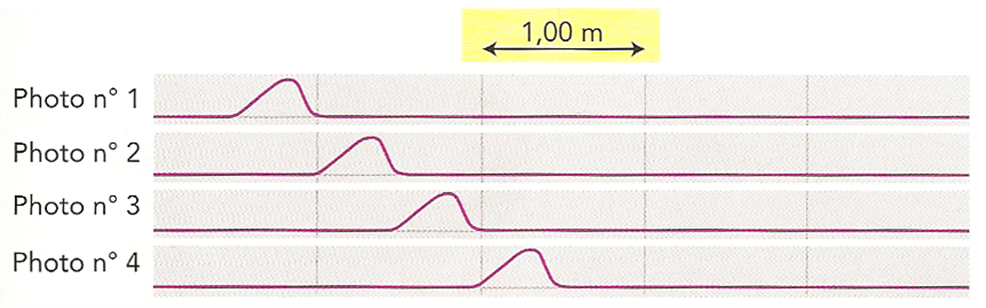
L’évolution au cours du temps des altitudes \(z_A\) et \(z_B\) de deux points \(A\) et \(B\) de la corde est représentée sur les schémas ci-dessus.

On note \(S\) le point situé à l’extrémité gauche de la corde. La date \(t_0 = \pu{0 s}\) correspond au début du mouvement de \(S\).

1 Définir la vitesse de propagation d’une onde. La calculer dans le cas de l'onde le long de la corde.

2 Pendant quelle durée un point de la corde est-il en mouvement ?

3 Lequel des points \(A\) et \(B\) est atteint le premier par la perturbation ?

4 Lequel de ces deux points est situé le plus près du point \(S\) de la corde ?

5 Avec quel retard le point touché en second reproduit-il le mouvement du point touché en premier ?

6 Quelle est la distance séparant les points \(A\) et \(B\) ?

7 Dessiner l’évolution au cours du temps d’un point \(C\) situé à \(\pu{1,5 m}\) de \(A\).