8.E16 : Longueur d’onde d’un laser vert

Des franges d’interférences sont réalisées sur un écran avec deux fentes parallèles séparées d’une distance \(b\). L’écran est à la distance \(D\) des fentes.

L’interfrange est notée \(i\).

Sur le graphique ci-dessous, les deux courbes représentent les fonctions \(i = f(D)\) obtenues, d’une part pour une diode laser rouge de longueur d’onde \(λ_R = \pu{650 nm}\) et d’autre part pour un laser vert de longueur d’onde \(λ_V\).

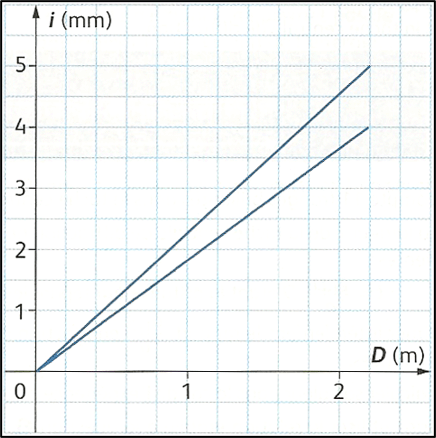
On rappelle que \(λ_V < λ_R\).

Par ailleurs, il est admis que pour les interférences, \(i = \dfrac{λ·D}{b}\) où \(λ·D\) est la distance entre les fentes et l’écran et \(b\) la distance entre les fentes.

1 Justifier l’allure des tracés.

2 Associer chaque courbe au laser correspondant.

3 Calculer la longueur d’onde \(λ_V\) du laser vert et déterminer la distance \(b\) entre les deux fentes.

Afficher la correction

1

D’après la relation \(i = \dfrac{λ·D}{b}\) on peut affirmer que \(i\) est proportionnelle à \(D\).

C’est bien ce que l’on observe sur le graphique car les deux courbes sont des droites qui passent par l’origine.

2

D’après la relation \(i = \dfrac{λ·D}{b}\) le coefficient directeur de la droite est \(\dfrac{λ}{b}\). Donc plus \(λ\) est grand plus le coefficient directeur est grand.

Or \(λ_V < λ_R\).

Donc la courbe du dessus est donc celle du laser rouge et la courbe du dessous celle du laser vert.

3

Notons \(k\) le coefficient directeur. \(k_V = \dfrac{λ_V}{b}\) et \(k_R = \dfrac{λ_R}{b}\). D’où \(λ_V = \dfrac{k_V}{k_R}·λ_R\).

Déterminons graphiquement les coefficients directeurs de chaque courbe :

- Pour la courbe du bas, avec le point A : \(k_V = \dfrac{\pu{0,004 m}}{\pu{2,2 m}} = \pu{1,8E–3}\).

- Pour la courbe du haut, avec le point B : \(k_R = \dfrac{\pu{0,004 m}}{\pu{1,8 m}} = \pu{2,2E–3}\).

Finalement :

\(\begin{align} λ_V &= \dfrac{k_V}{k_R}·λ_R \\ &= \dfrac{\pu{1,8E–3}}{\pu{2,2E–3}} × \pu{650} \\ &= \pu{530 nm} \end{align}\)