15.E23 : Mesure du faraday

On réaliser l'expérience dont le protocole est donné ci-dessous.

• - Peser les masses \(m_+\) et \(m_-\) de deux plaques de cuivre avec une balance de précision.
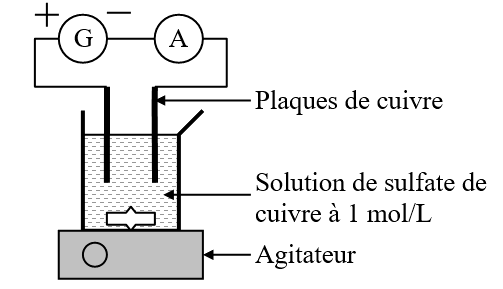
• - On réalise le dispositif du schéma ci-contre.
• - Régler le générateur pour qu'il délivre un courant d’intensité constante \(I = \pu{1,0 A}\).
• - Laisser fonctionner le montage pendant exactement \(\pu{10 min}\).
• - Rincer les électrodes. Les sécher correctement. Les peser.

Les résultats expérimentaux sont les suivants :

• - Plaque du côté de la borne + : \(m_+^{avant} = \pu{19,18 g}\) ; \(m_+^{apres} = \pu{18.99 g}\).
• - Plaque du côté de la borne – : \(m_–^{avant} = \pu{28,32 g}\) ; \(m_–^{apres} = \pu{28.51 g}\).

1 Déterminer l’anode (oxydation) et la cathode (réduction) en tenant compte des bornes du générateur et écrire les équations des demi-réactions qui se produisent à l’anode et à la cathode. En déduire la réaction globale de l'électrolyse.

2 A partir de la variation de masse de la cathode, déterminer la quantité de matière d’électron ayant circulé dans le circuit.

3 A partir de la valeur de l’intensité du courant et du temps de fonctionnement du dispositif, déterminer la quantité d’électricité Q ayant circulé dans le circuit.

4 En déduire la valeur du faraday.

5 Indiquer si la valeur trouvée est conforme à la valeur officielle.

Données :

Afficher la correction

1

Électrode de droite :

Les électrons arrivent à l'électrode de droite.

Donc la demi-équation qui se produit est : \(\ce{Cu^2+(aq) + 2 e^- -> Cu(s)}\). C'est une réduction (car \(\ce{Cu^2+}\) est un oxydant).

L'électrode de droite est donc la cathode.

Remarque : cette conclusion est cohérente avec le fait que la masse de cuivre du côté de la borne - augmente.

Électrode de gauche :

Les électrons partent de l'électrode de gauche.

Donc la demi-équation qui se produit est : \(\ce{Cu(s) -> Cu^2+(aq) + 2 e^-}\). C'est une oxydation (car \(\ce{Cu}\) est un réducteur).

L'électrode de gauche est donc l'anode.

Remarque : cette conclusion est cohérente avec le fait que la masse de cuivre du côté de la borne + diminue.

Équation globale : \(\ce{Cu(s) + Cu^2+(aq) -> Cu^2+(aq) + Cu(s)}\)

2

Masse de cuivre formé :

\(\begin{align} m_{formé}(\ce{Cu}) &= m_–^{après} - m_–^{avant} \\ &= \pu{28.51 g} - \pu{28,32 g} \\ &= \pu{0,19 g} \end{align}\)

Quantité de matière de cuivre formé :

\(\begin{align} n_{formé}(\ce{Cu}) &= \dfrac{n_{formé}(Cu)}{M(\ce{Cu})} \\ &= \dfrac{\pu{0,19 g}}{\pu{63,5 g*mol-1}} \\ &= \pu{3,0E-3 mol} \end{align}\)

Quantité de matière d'électrons échangés :

\(\begin{align} n(\ce{e^-}) &= 2 × n_{formé}(\ce{Cu}) \\ &= 2 × (\pu{3,0E-3 mol}) \\ &= \pu{6,0E-3 mol} \end{align}\)

3

Par définition, \(I = \dfrac{Q}{Δt}\).

\(\pu{10 min} = 10×60 = \pu{600 s}\)

D'où \(\begin{aligned}[t] Q &= I × Δt \\ &= (\pu{1,0 A}) × (\pu{600 s}) \\ &= \pu{600 C} \end{aligned}\)

4

On a \(Q = n(e^-) × F\)

D'où \(\begin{aligned}[t] F &= \dfrac{Q}{n(e^-)} \\ &= \dfrac{\pu{600 C}}{\pu{6,0E-3 mol}} \\ & = \pu{1,0E5 C*mol-1} \end{aligned}\)

5

La valeur trouvée expérimentalement est proche de la valeur théorique.