15.E11 : Pile et concentration

On réalise une pile avec les couples \(\ce{Ag+(aq) / Ag(s)}\) et \(\ce{Fe3+(aq) / Fe^2+(aq)}\) comme schématisé ci-dessous.

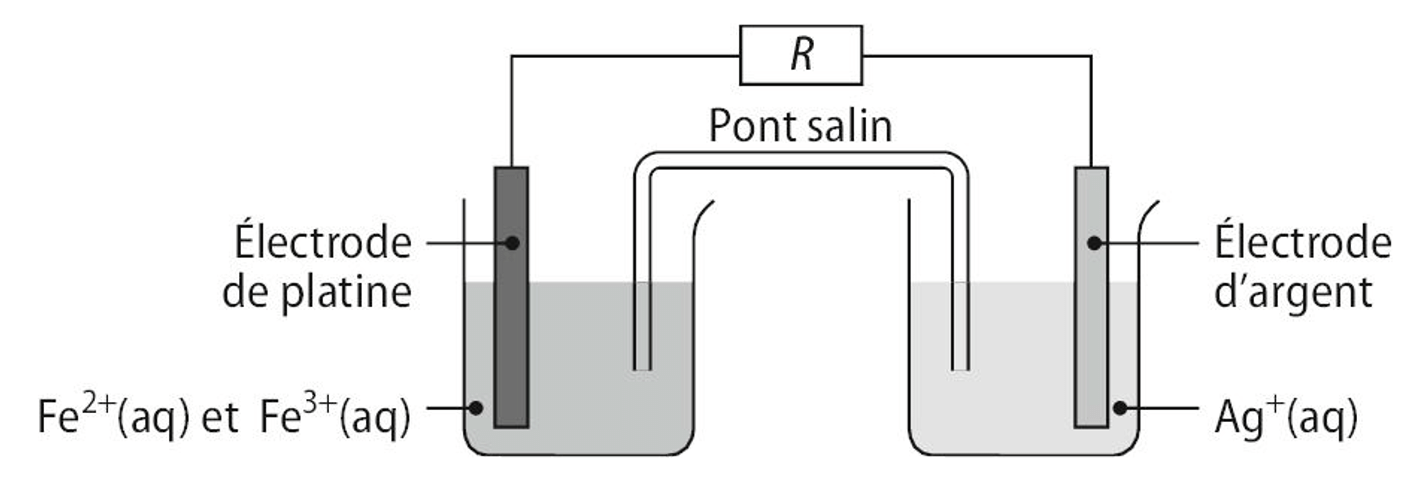
Les concentrations en quantité de matière initiales des ions dans les demi-piles sont : \([\ce{Ag+}]_i = [\ce{Fe^2+}]_i = [\ce{Fe^3+}]_i = \pu{1,0E–1 mol*L–1}\).

La constante d’équilibre associée à la réaction dont l’équation est \(\ce{Ag+(aq) + Fe^2+(aq) <--> Ag(s) + Fe^3+(aq)}\) vaut \(K(T) = \pu{3,2}\) à \(\pu{25 °C}\).

1 Calculer le quotient de réaction à l’état initial.

2 En déduire le sens d’évolution spontané de la transformation quand la pile fonctionne.

3 En justifiant avec les demi-équations électroniques, indiquer le sens de circulation des électrons à l’extérieur de la pile et préciser la polarité de la pile.

4 On réalise une deuxième pile en modifiant les concentrations initiales en quantité de matière : \([\ce{Ag+}]_i = [\ce{Fe^2+}]_i = \pu{1,0E–1 mol*L–1}\) ; \([\ce{Fe^3+}]i = \pu{1,0E–2 mol*L–1}\).

Justifier si la polarité de la pile reste la même.

Afficher la correction

\(Q_{r,i} = \dfrac{1^1 × \left(\dfrac{[\ce{Fe^3+}]_i}{c^0}\right)^1}{\left(\dfrac{[\ce{Fe^2+}]_i}{c^0}\right)^1×\left(\dfrac{[\ce{Ag+}]_i}{c^0}\right)^1}\)

En \(\pu{mol*L-1}\) on obtient :

\(\begin{align} Q_{r,i} &= \dfrac{[\ce{Fe^3+}]_i}{[\ce{Fe^2+}]_i×[\ce{Ag+}]_i} \\ &= \dfrac{(\pu{1,0E-1})}{(\pu{1,0E-1})×(\pu{1,0E-1})} \\ &= \pu{10} \end{align}\)

\(Q_{r,i} > K\) donc l'évolution spontanée du système se fait dans le sens indirect.

Du côté gauche :

La demi-équation est : \(\ce{Fe^3+ + e- -> Fe^2+}\).

Donc les \(\ce{e-}\) arrivent et c'est une réduction.

Donc le courant part.

Donc c'est le pôle + de la pile.

Du côté droit :

La demi-équation est : \(\ce{Ag -> Ag+ + e-}\).

Donc les \(\ce{e-}\) partent et c'est une oxydation.

Donc le courant arrive.

Donc c'est le pôle -.

\(\begin{align} Q_{r,i} &= \dfrac{[\ce{Fe^3+}]_i}{[\ce{Fe^2+}]_i×[\ce{Ag+}]_i} \\ &= \dfrac{(\pu{1,0E-2})}{(\pu{1,0E-1})×(\pu{1,0E-1})} \\ &= \pu{1} \end{align}\).

\(Q_{r,i} < K\) donc l'évolution spontanée du système se fait dans le sens direct.

Les polarités de la pile sont inversées.