Chap12 : Évolution temporelle dans un circuit capacitif
I - Rappels d’électricités
II - Régime variable
1 - Présentation
En régime continu, les grandeurs électriques sont constantes au cours du temps. C’est le régime qui a été étudié les années précédentes.
En régime variable, les grandeurs électriques varient au cours du temps et sont algébriques (elles peuvent être positives ou négatives).
Usuellement, on les note avec des minuscules : \(u(t)\), \(i(t)\)... ou plus simplement \(u\), \(i\)...
2 - Courant électrique en régime variable
a - Rappel : relation entre la charge et l'intensité du courant en régime statique
\(I\) est la charge positive qui traverse une section de fil par unité de temps.
Autrement dit : \(I = \dfrac{Q}{Δt}\), avec \(I\) en ampères (\(\pu{A}\)) ; \(Q\) en coulombs (\(\pu{C}\)) ; \(Δt\) en secondes (\(\pu{s}\)).
Remarque : \(\pu{C}\) est équivalent à \(\pu{A·s}\).
d - Signe de \(i(t)\) en régime variable
En régime variable, on définit un courant \(i(t)\) en précisant bien son sens.
Par exemple :

Alors, par convention :
- - \(i(t) > 0\) lorsque les charges + se déplacent dans le sens de la flèche (de A vers B).
- - \(i(t) < 0\) lorsque les charges + se déplacent dans le sens opposé à la flèche (de B vers A).
c - Relation pour \(i(t)\) en régime variable
Notons \(q(t)\) la charge qui a traversé une section de fil à un instant \(t\).
Notons \(i(t)\) l’intensité du courant.
La relation du a) s’écrit : \(i(t)=\dfrac{q(t+Δt)-q(t)}{Δt}\)
A un instant donné, \(i(t)\) n’a de sens que si on prend un intervalle de temps le plus petit possible, c’est-à-dire qu’on prend \(Δt → 0\).
On voit donc que \(i(t)\) est la dérivée de \(q(t)\). Soit \(i(t)=\dfrac{dq(t)}{dt}\) ou plus simplement : \(i=\dfrac{dq}{dt}\).
III - Modèle du condensateur
1 - Comportement capacitif
Expérience de présentation :
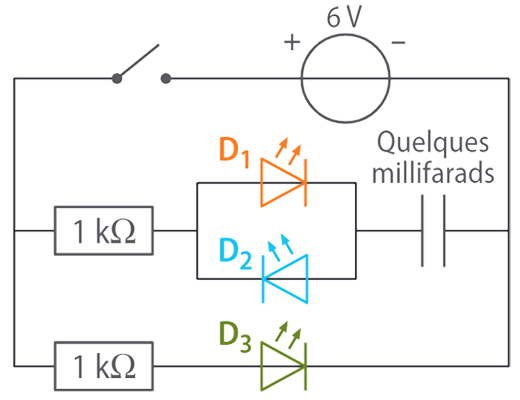
2 - Définition et propriété
• Un condensateur est un ensemble de deux armatures conductrices placées face à face, et séparées par un isolant.
• Les deux armatures d’un condensateur portent des charges électriques opposées.
Remarque : le condensateur est globalement électriquement neutre à chaque instant.
3 - Lien entre \(q\) et \(i\)
Considérons le schéma ci-contre.
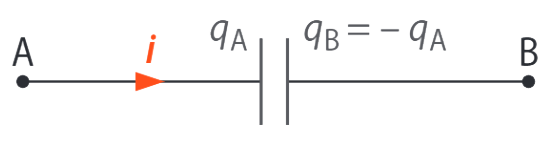
S’il y a un courant \(i > 0\) :
- => des charges + arrivent sur l’armature A et partent de l’armature B,
- => la charge \(q_A\) augmente.
4 - Capacité d’un condensateur
a - Définition et relation
Du fait de l’accumulation de charges sur les armatures, il existe une tension entre les armatures.
On montre que la charge accumulée est proportionnelle à la tension. Le coefficient de proportionnalité est appelé capacité du condensateur.
La capacité d’un condensateur se note \(C\) et s’exprime en farad (\(\pu{F})\).
Rq : \(\pu{F}\) est équivalent à \(\pu{C}·\pu{V}^{-1}\).
On travaille en convention récepteur (\(q\) du côté de la pointe de la tension).
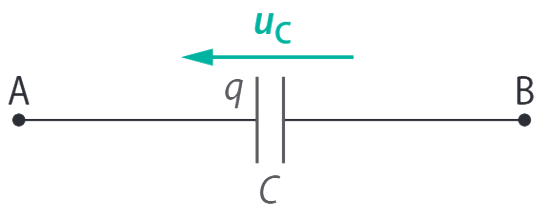
On a la relation \(q = C·u_C\) avec \(q\) en coulombs (\(\pu{C}\)) ; \(C\) en farads (\(\pu{F}\)) ; \(u_C\) en volts (\(\pu{V}\)).
b - Quelques valeurs
En électronique, les capacités des condensateurs utilisés sont petites \(\pu{mF}\) ou \(\pu{µF}\), voir \(\pu{nF}\).
Les plus grosses valeurs sont de l’ordre du \(\pu{F}\) (mais ces condensateurs sont très peu utilisés).
5 - Relation courant-tension du condensateur
a - Relation
On travaille en convention récepteur.
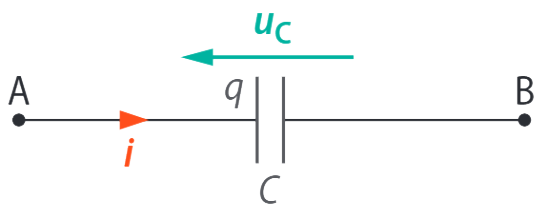
Relation : \(i = C·\dfrac{du_C}{dt}\) avec \(i\) en ampères (A), \(C\) en farads (F) ; \(u\) en volts (V) ; \(t\) en secondes (s).
Établissement de la relation :
- On a \(q = C·u_C\) et \(i = \dfrac{dq}{dt}\)
- Donc \(i = \dfrac{d(C·u_C)}{dt}\). Soit \(i = C·\dfrac{du_C}{dt}\).
b - Continuité de la charge et de la tension au cours du temps
Les charges ne peuvent pas se déplacer instantanément.
Donc la charge \(q(t)\) ne varie jamais par saut, mais uniquement de façon continue.
En conséquence, \(u_C(t)\) ne varie jamais par saut non plus, mais également uniquement de façon continue.
IV - Charge d'un condensateur dans un circuit RC
1 - Circuit
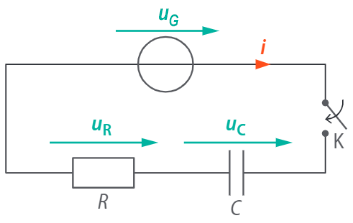
2 - Equation différentielle pour \(u_C\)
Loi des nœuds : \(i\) est le même dans tout le circuit
Loi des mailles : \(u_G = u_R + u_C\)
Lois pour les dipoles :
- • résistance : \(u_R = R·i\)
- • générateur : \(u_G = E\)
- • condensateur : \(i = C·\dfrac{du_C}{dt}\)
Bilan :
- On obtient l'équation : \(E = RC·\dfrac{du_C}{dt} + u_C\)
- Soit aussi : \(\dfrac{du_C}{dt} = -\dfrac{1}{RC}·u_C + \dfrac{E}{RC}\)
- Il s’agit d’une équation différentielle linéaire du premier ordre.
3 - Résolution de l’équation différentielle
a - Lien avec les math :
L’équation est de la forme \(y’ = a·y+b\). C’est une équation différentielle linéaire du premier ordre.
Solution particulière : c’est une solution de \(0 = a·y + b\). Soit \(y_0 = -b/a\).
Solution de l’équation homogène (c’est à dire de \(y’ = a·y\)) : \(y_1 = C·exp(a·x)\).
Solution générale, c'est la somme des deux solutions précédentes : \(y = C·exp(a·x)-b/a\).
Les conditions initiales permettent de déterminer C.
b - En physique :
La variable est \(t\).
Solution particulière : \(u_C = E\).
Solution de l’équation homogène : \(u_C = A·exp(-\dfrac{t}{R·C})\).
Solution générale : \(u_C = A·exp(-\dfrac{t}{R·C}) + E\).
Condition initiale : \(u_C(t=0) = 0\). D’où \(A = -E\).
Bilan : \(u_C(t) = E·\left(1-exp(-\dfrac{t}{R·C})\right)\).
4 - Temps caractéristique de charge
a - Définition
Le temps caractéristique d’évolution (aussi appelé constante de temps du circuit RC) est défini comme le montre le schéma ci-dessous. On le note \(τ\), il s’exprime en secondes (\(\pu{s}\)).
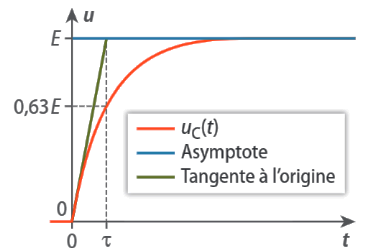
b - Calcul
On montre que : \(τ = RC\).
c - Mesure
Quand \(t = τ\), \(u_C = 0,63·E\).
d - Temps de charge complète
On peut considérer que le condensateur est totalement chargé pour \(t = 5·τ\).
En effet : \(\begin{aligned}[t] u_C(5τ) &= E·(1-exp(-\dfrac{5τ}{τ}) \\ &= E·(1-exp(-5)) \\ &= 0,993·E \end{aligned}\).
5 - Intensité du courant
Méthode 1 (avec la résistance)
On a : \(i = \dfrac{u_R}{R}\).
Or \(u_R = E – u_C\).
D’où \(i = \dfrac{E-u_C}{R}\).
Soit : \(i = \dfrac{E}{R}·exp(-\dfrac{t}{τ})\).
Méthode 2 (avec la dérivée)
On a : \(i = C·\dfrac{du_C}{dt}\).
Or \(\begin{aligned}[t] \dfrac{du_C}{dt} &= \dfrac{d}{dt}\left( E·-E·exp(-\dfrac{t}{R·C}) \right) \\ &= (-\dfrac{1}{τ})·(-E·exp(-\dfrac{t}{τ})) \\ &=\dfrac{E}{τ}·exp(-\dfrac{t}{τ}) \end{aligned}\).
Soit \(\begin{aligned}[t] i &= C·\dfrac{E}{τ}·(exp(-\dfrac{t}{τ})) \\ &= C·\dfrac{E}{RC}·exp(-\dfrac{t}{τ}) \end{aligned}\).
Soit : \(i = \dfrac{E}{R}·exp(-\dfrac{t}{τ})\).
6 - Charge portée par les armatures du condensateur
On a : \(q=C·u_C\)
Soit : \(q = C·E·\left(1-exp\left(-\dfrac{t}{τ}\right)\right)\).
V - Décharge du condensateur
1 - Circuit
On choisit la convention récepteur pour la résistance et le condensateur.
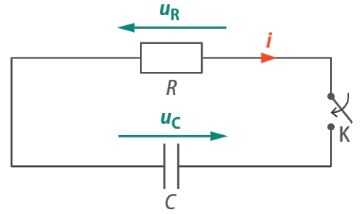
On considérera qu'à \(t = 0\), \(u_C = U_0\).
2 - Equation différentielle pour \(u_C\)
On trouve : \(R·C·\dfrac{du_C}{dt} + u_C = 0\).
Soit : \(\dfrac{du_C}{dt}=-\dfrac{u_C}{R·C}\).
Il s’agit d’une équation différentielle linéaire du premier ordre homogène.
3 - Résolution de l'équation différentielle
La variable est \(t\).
La solution générale : \(u_C=A·exp(-\dfrac{t}{τ})\).
Condition initiale : \(u_C(t=0) = U_0\). D'où \(A=U_0\).
Bilan : \(u_C(t) = U_0·exp(-\dfrac{t}{τ})\).
4 - Temps caractéristique de décharge
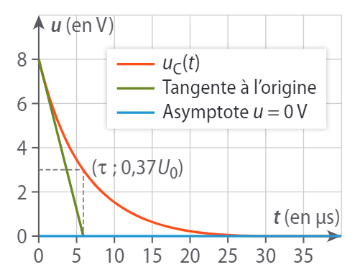
• On montre que, là encore : \(τ=R·C\).
• Quand \(t = τ\), \(u_C = 0,37·U_0\).
• On peut considérer que le condensateur est totalement déchargé pour \(t = 5·τ\).
En effet \(u_C(5τ) = U_0·exp(-\dfrac{5τ}{τ}) = U_0·exp(-5) = 0,0067·U_0\).
5 - Intensité du courant
Méthode 1 (avec la résistance)
D'après le circuit \(u_C = -u_R\).
Or \(u_R = R·i\)
d'où \(i(t) = \dfrac{u_R}{R}\). Soit \(i(t) = - \dfrac{u_C}{R}\).
D'où : \(i(t)=-\dfrac{U_0}{R}·exp(-\dfrac{t}{τ})\).
Remarque : comme on a choisi la convention récepteur et que l'intensité du courant est négative, cela signifie que les charges + vont dans le sens de la tension \(u_C\).
Méthode 2 (avec la dérivée)
On a : \(i = C·\dfrac{du_C}{dt}\).
Or \(\dfrac{du_C}{dt}=(-\dfrac{1}{τ})·U_0·exp(-\dfrac{t}{τ})\).
Soit \(\dfrac{du_C}{dt}=-\dfrac{U_0}{τ}·exp(-\dfrac{t}{τ})\).
Soit \(i = -C·\dfrac{U_0}{τ}·(exp(-\dfrac{t}{τ})\).
Soit \(i = -C·\dfrac{U_0}{RC}·exp(-\dfrac{t}{τ})\).
Soit : \(i = -\dfrac{U_0}{R}·exp(-\dfrac{t}{τ})\).
6 - Charge portée par les armatures du condensateur
On a : \(q=C·u_C\)
Soit : \(q = C·U_0·exp(-\dfrac{t}{τ})\).
Remarque : \(C·U_0 = q_0\), c'est-à-dire la charge portée par l'armature positive à l'instant \(t=0\).
VI - Capteur capacitif
1 - Quelques capteurs en lien avec les résistances (rappels)
Les résistances sont utilisées dans nombreux capteurs :
- - capteur de température (thermistance),
- - capteur de lumière,
- - ...
2 - Capteurs capacitifs
Les condensateurs, sous des formes variées, sont utilisés dans un nombre très varié de capteurs :
- - capteur de petits déplacements (variation de la distance entre les armatures),
- - microphone capacitif (variation de la distance entre les armatures),
- - capteur de niveau de liquide (modification de l'isolant entre les armatures) => Vidéo (youtube),
- - capteur tactile, par exemple dans certaines technologies d'écrans tactiles,
- - ...
