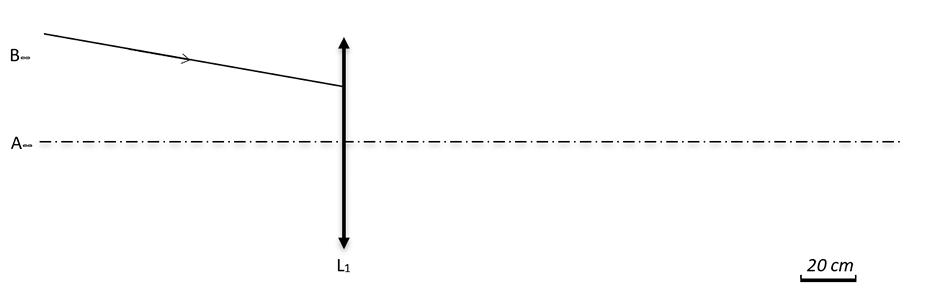
11.E7 : Modélisation d’une lunette astronomique

On décide de modéliser une lunette en utilisant deux lentilles convergentes :

• - l’objectif : lentille L1 de distance focale \(f’_1\) égale à \(\pu{1,0 m}\) et de diamètre \(\pu{6 cm}\) ;
• - l’oculaire : lentille L2 de distance focale \(f’_2\) égale à \(\pu{20,0 cm}\) et de diamètre \(\pu{6 cm}\).

1 Où se situe l'image par l'objectif d'un objet à l'infini ? Cette image est appelée image intermédiaire.

2 Où doit se situer l'image intermédiaire pour être vue à travers l'oculaire sans accommoder ?

3 Préciser la position du foyer objet \(F_2\) de l'oculaire par rapport au foyer image \(F’_1\) de l'objectif.

4 Placer la lentille L2 sur la figure ci-dessous (échelle \(\pu{{1/20}^{ème}}\)).

5 Construire l'image \(A_1B_1\), dite image intermédiaire, de \(AB\) par L1 puis l'image \(A_2B_2\) de \(A_1B_1\) par L2.

6 Le diamètre apparent de l'objet AB situé à l'infini est noté \(\theta\) et celui de l'image définitive \(A_2B_2\) est noté \(\theta'\).

Afficher la correction

1

L'image par l'objectif d'un objet à l'infini se trouve dans le plan focal image de la lentille L1.

2

Pour ne pas avoir à accommoder, l'image intermédiaire doit se trouver dans le plan focal objet de la lentille L2, ainsi l'image formée est à l'infini.

3

L foyer objet \(F_2\) de l'oculaire est confondu avec le foyer image \(F’_1\) de l'objectif.

4 5

et 6.2

6

6.1

Le diamètre apparent d'un objet et l'angle entre le rayon émis par le point le plus excentré de l'objet qui pénètre dans l'œil et l'axe optique.

6.2

Voir schéma ci-dessus.

6.3

Établissement de la relation donnant le grossissement \(G\)

On travaille dans l'approximation des petits angles. Donc \(tan(\theta) = \theta\) et \(tan(\theta') = \theta'\)

Par définition \(G = \dfrac{\theta'}{\theta}\).

D'une part on a : \(tan(\theta) = \dfrac{A_1B_1}{f'_1}\). Soit \(A_1B_1 = f'_1 × tan(\theta)\). Et donc \(A_1B_1 = f'_1 × \theta\).

D'autre part on a : \(tan(\theta') = \dfrac{A_1B_1}{f'_2}\). Soit \(A_1B_1 = f'_2 × tan(\theta')\). Et donc \(A_1B_1 = f_2' × \theta'\).

Finalement : \(f'_1 × \theta = f'_2 × \theta'\)

Soit \(\dfrac{\theta'}{\theta} = \dfrac{f'_1}{f'_2}\)

Soit \(G = \dfrac{f'_1}{f'_2}\)

Ici :

\(\begin{align} G &= \dfrac{\pu{1,0 m}}{\pu{0,20 m}} \ &= \pu{5,0} \end{align}\)

Graphiquement, à l'aide d'un rapporteur, on trouve :

\(\theta = \pu{\pu{9 °}}\)

\(\theta' = \pu{\pu{42 °}}\)

Soit \(G = \dfrac{42}{9} = \pu{4,7}\)