11.E6 : Modélisation d’une lentille

Soit la lentille L, de distance focale f’ égale à \(\pu{2,0 cm}\).

1 Par quelle relation définit-on la distance focale d'une lentille ?

2 Calculer la vergence \(C\) de cette lentille.

3 Compléter la figure ci-dessous (échelle 1) avec l’axe optique \(∆\), le centre optique \(O\), le foyer image \(F’\) et le foyer objet \(F\).

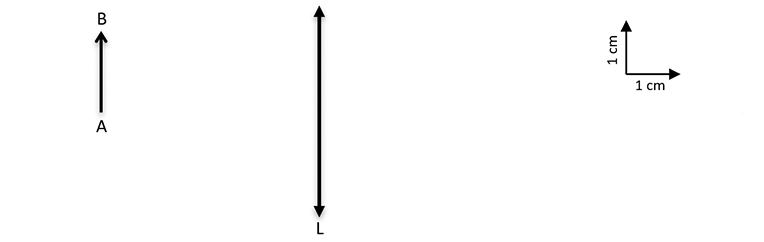
4 Construire l'image \(A’B’\) par la lentille L de l'objet \(AB\).

5 On souhaite vérifier la taille de l'image \(A’B’\) par le calcul.

Données : \(OA = \pu{4,0 cm}\) ; \(AB = \pu{1,5 cm}\).

5.a Utiliser la formule de conjugaison pour déterminer la position de l'image \(A’B’\).

5.b Utiliser la formule du grandissement pour déterminer la taille de l'image \(A’B’\).

Afficher la correction

La distance focale est la distance entre le centre optique et le foyer images.

\(C = \dfrac{1}{f'}\) où \(C\) est en \(\pu{\delta}\) et \(f'\) en \(\pu{m}\).

Soit ici \(C = \dfrac{1}{\pu{0,020 m}} = \pu{50 \delta}\)

2 et 2

5.a

La relation de conjugaison est : \(\dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}} = \dfrac{1}{f'}\)

D'où \(\overline{OA'} = \dfrac{1}{\dfrac{1}{f'}+\dfrac{1}{\overline{OA}}}\)

Soit \(\overline{OA'} = \dfrac{1}{\dfrac{1}{\ce{2,0 cm}}+\dfrac{1}{\pu{-4,0 cm}}}\)

Soit \(\overline{OA'} = \pu{4,0 cm}\)

5.b

Les formules pour le grandissement permettent d'écrire : \(\dfrac{\overline{OA'}}{\overline{OA}} = \dfrac{\overline{A'B'}}{\overline{AB}}\)

D'où \(\overline{A'B'} = \overline{AB} × \dfrac{\overline{OA'}}{\overline{OA}}\)

Soit \(\overline{A'B'} = \pu{1,5 cm} × \dfrac{\pu{4,0 cm}}{\pu{-4,0 cm}}\)

Soit \(\overline{A'B'} = \pu{-1,5 cm}\)