Chap11 : La lunette astronomique
I - Quelques rappels
1 - Les éléments d’une lentille mince
a - Éléments géométriques
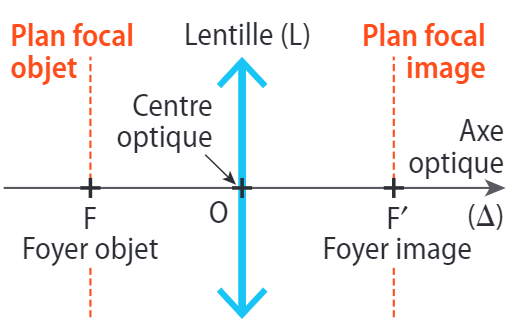
b - Caractéristiques
Distance focale \(f’\) : \(f' = \overline{OF’}\)
Vergence \(C\) : \(C = 1/f’\). \(C\) s’exprime en dioptrie (\(\delta\)), \(\pu{1 \delta} = \pu{1 m^{–1}}\).
2 - Objet, image, tracé des rayons pour une lentille convergente
a - Tracé des rayons
■ Tout rayon parallèle à l’axe optique ressort de la lentille en passant par le foyer principal image \(F’\).
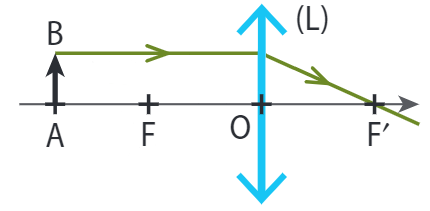
■ Tout rayon passant par le foyer principal objet \(F\) ressort de la lentille parallèlement à l’axe optique.
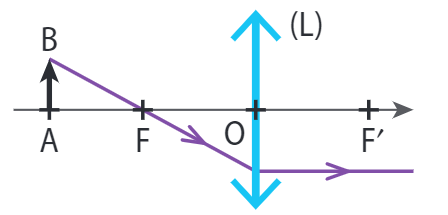
■ Tout rayon passant par le centre optique O ressort de la lentille sans être dévié.
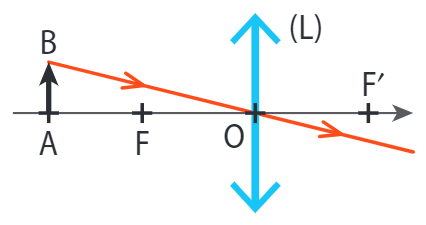
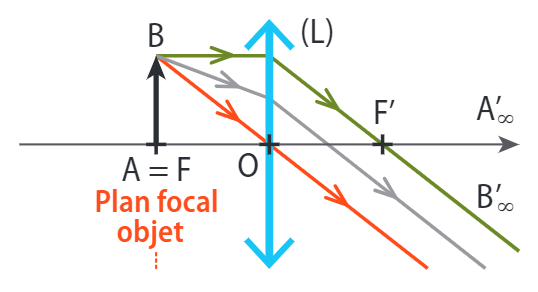
b - Objet à l’infini
Un objet est à l’infini (avant la lentille) lorsque les rayons qu’il émet sont parallèles.
Son image est dans le plan focal image de la lentille.
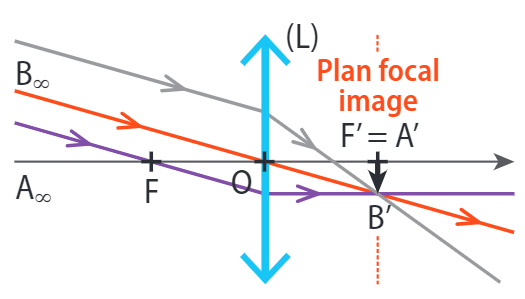
c - Image à l'infini
Une image est à l’infini (après la lentille) lorsque les rayons qui ressortent de la lentille sont parallèles.
L'objet d'une image à l'infini est dans le plan focal objet de la lentille.
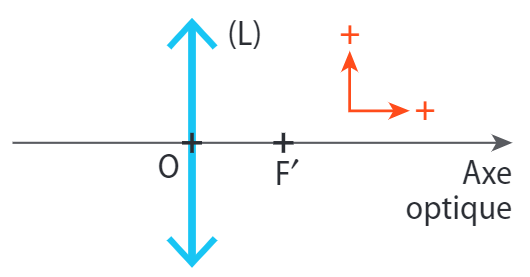
3 - Grandeurs algébriques
L’axe optique est orienté dans le sens de propagation de la lumière.
L’axe perpendiculaire à l’axe optique est en général orienté positivement vers le haut.
En optique, on travaille avec des grandeurs algébriques.
4 - Formules pour les lentilles minces
a - Grandissement
Le grandissement se note \(γ\), c’est une grandeur sans unité. \(γ=\dfrac{\overline{A'B'}}{\overline{AB}}\) ou \(γ=\dfrac{\overline{OA'}}{\overline{OA}}\)
b - Relation de conjugaison
La relation de conjugaison de Descartes est : \(\dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}=\dfrac{1}{f'}\)
II - La lunette astronomique
1 - Définition
Une lunette astronomique forme, d’un objet à l’infini, une image à l’infini.
C’est un système afocal, c’est-à-dire sans foyer.
2 - Modèle optique d’une lunette astronomique
a - Constitution de la lunette
Une lunette astronomique est constituée de deux lentilles convergentes :
- • L’objectif : du côté de l’objet placé à l’infini ;
- • L’oculaire : du côté de l’œil qui reçoit les rayons sans accommoder.
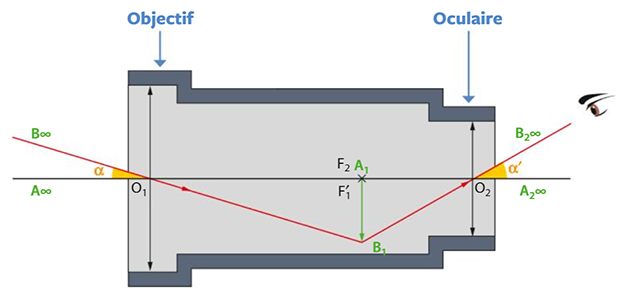
b - Rôle de l'objectif et de l'oculaire
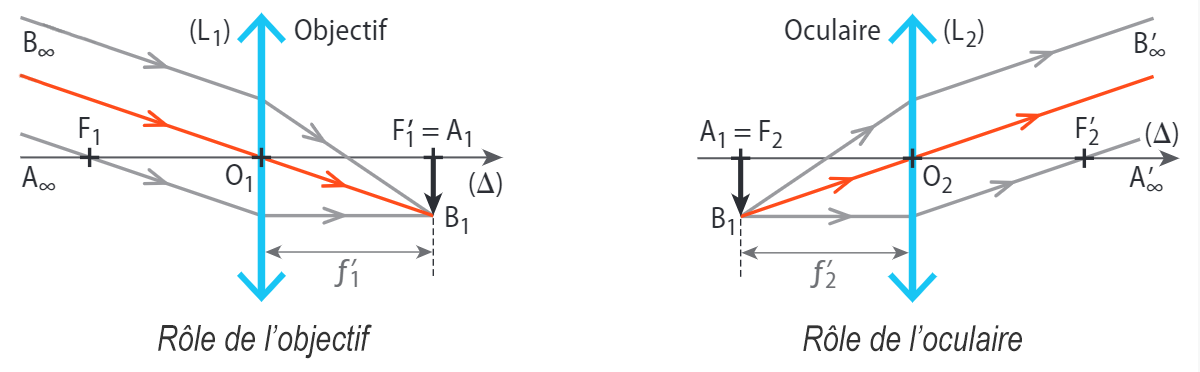
c - Réglage de la lunette
La lunette est réglée lorsqu’elle constitue un système afocal.
Dans ce cas, le foyer image de l’objectif est confondu avec le foyer objet de l’oculaire.
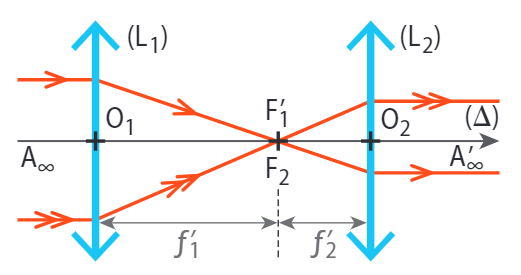
3 - Grossissement
a - Vocabulaire : diamètre apparent d’un objet
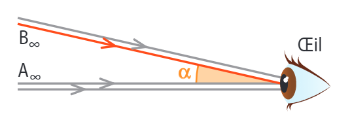
Le diamètre apparent d’un objet placé à l’infini est l’angle sous lequel l’œil voit cet objet.
C'est l'angle entre le rayon émis par le point le plus excentré de l'objet qui pénètre dans l'œil et l'axe optique.
b - Définition du grossissement
Considérons un point placé à l’infini.
Notons \(α\) l’angle que font les rayons issus de ce point et entrant dans la lunette avec l’axe optique de la lunette.
Notons \(α’\) l’angle que font les rayons issus de ce point et sortant de la lunette
Le grossissement, noté \(G\), c’est une grandeur sans dimension.
\(G = \dfrac{α’}{α}\)
Remarque : \(G\) est également le rapport des diamètres apparents d’un objet placé à l’infini vu avec et sans la lunette.
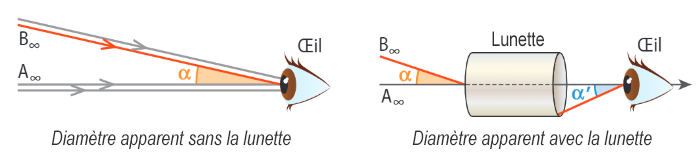
c - Formule du grossissement
■ Formule :
\(G = \dfrac{f’_{objectif}}{f’_{oculaire}}\)
■ Démonstration :
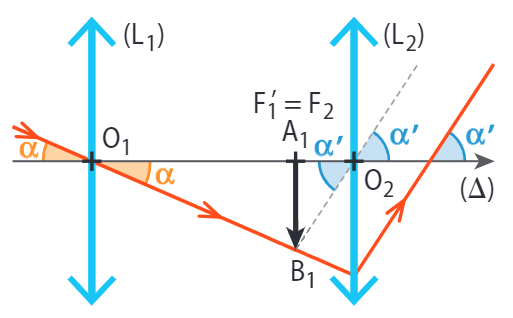
• Dans le triangle \(O_1A_1B_1\) :
- On a : \(tan(α) = \dfrac{A_1B_1}{O_1A_1} = \dfrac{A_1B_1}{f’_1}\).
- Soit, dans l’approximation des petits angles \(α = \dfrac{A_1B_1}{f’_1}\).
• Dans le triangle \(O_2A_1B_1\) :
- On a : \(tan(α') = \dfrac{A_1B_1}{O_2A_1} = \dfrac{A_1B_1}{f’_2}\).
- Soit, dans l’approximation des petits angles \(α' = \dfrac{A_1B_1}{f’_2}\).
• \(G = \dfrac{α’}{α}\). Soit \(G = \dfrac{\dfrac{A_1B_1}{f’_2}} {\dfrac{A_1B_1}{f’_1}}\). Soit \(G = \dfrac{f’_1}{f’_2}\).
