8.E11 : Mesure de la taille d’une fente

Un laser Hélium-néon émet une lumière rouge de longueur d’onde dans le vide \(\lambda = \pu{633 nm}\).

Une fente de larguer \(a\) est placée sur le trajet du faisceau lumineux produit par le laser.

Un écran est placé à la distance \(D = \pu{2,00 m}\) de la fente.

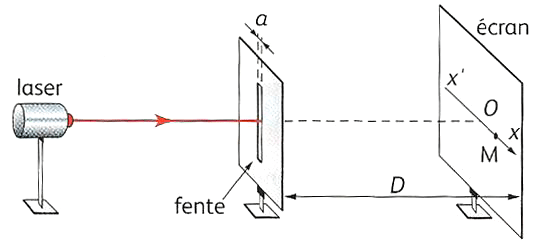
On déplace une cellule photoélectrique le long de l’axe \((x’x)\) d’origine \(O\). Cette cellule délivre une tension \(u\) proportionnelle à l’intensité lumineuse au point \(M\) d’abscisse \(x\). On obtient la courbe de mesures suivantes.

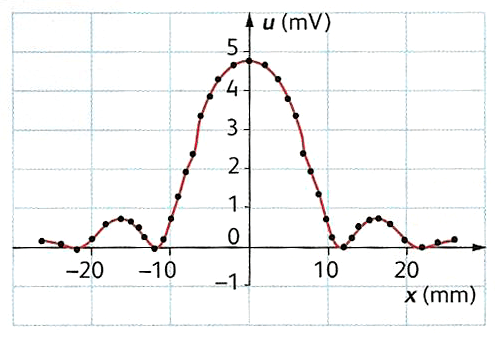
1 Déterminer, à l’aide de la courbe, la largeur de la tâche centrale.

2 La largeur \(L\) de la tache centrale de diffraction est donnée par la relation \(L = \dfrac{2·\lambda·D}{a}\). Déterminer la valeur de la largeur de la fente \(a\).

Afficher la correction

D’après le graphique, la deuxième extinction est à \(\pu{22 mm}\).

Donc \(2 × \dfrac{L}{2} = \pu{22 mm}\).

Soit \(L = \pu{22 mm} = \pu{0,022 m}\).

Ici \(\lambda = \pu{633 nm} = \pu{633E–9 m}\).

D’après la relation de l'énoncé, on obtient :

\(\begin{align} a &= \dfrac{2·\lambda·D}{L} \\ &= \dfrac{2×(\pu{633E–9 m})×(\pu{2,00 m})}{(\pu{0,022 m})} \\ &= \pu{1,15E–4 m} \end{align}\)