Chap08 : Ondes et phénomènes ondulatoires
I - Ondes
1 - Qu’est-ce qu’une onde ?
Onde progressive : Une onde progressive est la propagation de proche en proche d'une perturbation.
Onde mécanique ou onde électromagnétique : Il existe deux types d’ondes progressives :
- - Les ondes électromagnétiques, comme la lumière, qui se propagent dans le vide ;
- - Les ondes mécaniques, comme les ondes sonores, qui ont besoin d’un support matériel pour se propager.
2 - Célérité et retard
La célérité d'une onde est la vitesse à laquelle se propage la perturbation. On la note \(v_{onde}\) ou \(c\).
Le retard entre deux points A et B est le temps au bout duquel la perturbation arrive B après être passée par A.
Retard = Distance / Célérité
3 - Ondes progressives périodiques
a - Période et fréquence
Période :
- - la période se note \(T\) et s’exprime en \(\pu{s}\).
- - La période est le temps au bout duquel, en un point donné, le phénomène se répète.
Fréquence :
- - La fréquence se note \(f\) ou \(N\) et s’exprime en hertz (\(\pu{Hz}\))
- - La fréquence est le nombre de répétition par seconde.
Relation entre \(T\) et \(f\) : On a \(T = \dfrac{1}{f}\) ou \(f = \dfrac{1}{T}\).
b - Longueur d’onde
La longueur d’onde se note \(λ\) et s’exprime en \(\pu{m}\).
La longueur d’onde est la distance au bout de laquelle le motif de l’onde se répète.
c - Relation entre \(λ\) et \(T\)
Relation entre la longueur d’onde et la période : \(λ = célérité × T\) ou \(λ = \dfrac{célérité}{f}\).
II - Ondes électromagnétiques périodiques
Les ondes électromagnétiques sont des ondes progressives.
Elles n’ont pas besoin d’un milieu matériel pour se propager, elles se propagent dans le vide comme dans la matière.
Dans le vide, leur célérité est \(c = \pu{299 792 458 m*s-1}\). Soit \(c = \pu{3,00E8 m*s-1}\).
Les ondes électromagnétiques ont des usages différents suivant leur longueur d'onde :
Sur ostralo.net : Les ondes électromagnétiques
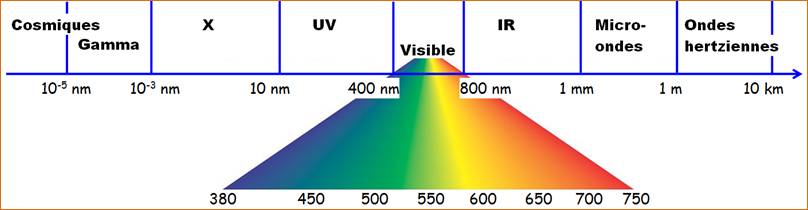
La lumière visible est un ensemble d'ondes électromagnétiques dont le domaine des longueurs d'onde est compris entre \(\pu{400 nm}\) et \(\pu{750 nm}\).
III - Cas des ondes sonores
1 - Rappels
Les ondes sonores sont des ondes mécaniques progressives.
Elles correspondent à une modification de proche en proche de la pression du milieu de propagation.
Spectre des ondes sonores :

Dans l’air, la célérité du son est \(c = \pu{340 m*s-1}\).
2 - Niveau d’intensité sonore
a - Intensité sonore
L’intensité sonore se note \(I\), elle s’exprime en \(\pu{W*m^–2}\).
L'intensité sonore est la puissance par unité de surface : \(I = \dfrac{P}{S}\).
Remarque : on note \(I_0\) le niveau d’intensité sonore de référence. \(I_0 = \pu{1,0E-12 W*m^-2}\)
b - Niveau d'intensité sonore
Le niveau d’intensité sonore se note \(L\), il s’exprime en \(\pu{dB}\).
c - Relation entre \(I\) et \(L\)
\(L = 10 \times log\left(\frac{I}{I_0}\right)\) et \(I = I_0 \times 10^{\left(\frac{L}{10}\right)}\).
3 - Atténuation
a - Définition
L’atténuation se note \(A\) et s’exprime en \(\pu{dB}\). Elle donne une comparaison entre la force d'une onde sonore à l'entrée et à la sortie d'une zone de propagation.
L’atténuation est définie par : \(A = L_{sortie} - L_{entree} = 10 \times log\left(\dfrac{I_{sortie}}{I_{entree}}\right)\)
b - Causes de l’atténuation
• Atténuation géométrique
Lorsqu’une onde se propage dans toutes les directions, l’énergie se répartit sur une surface de plus en plus grande.
• Atténuation par absorption
Lorsqu’une onde sonore se propage dans un milieu absorbant, une partie de l’énergie est transférée au milieu.
IV - Diffraction
1 - Généralités
Lorsqu’une onde mécanique ou lumineuse rencontre une ouverture ou un obstacle de petite taille par rapport à sa longueur d’onde, on observe un étalement des directions de propagation de l’onde.
Lorsque ce phénomène se produit, l’onde conserve sa fréquence (et donc sa période), ainsi que sa longueur d’onde.
2 - Exemple avec la cuve à onde
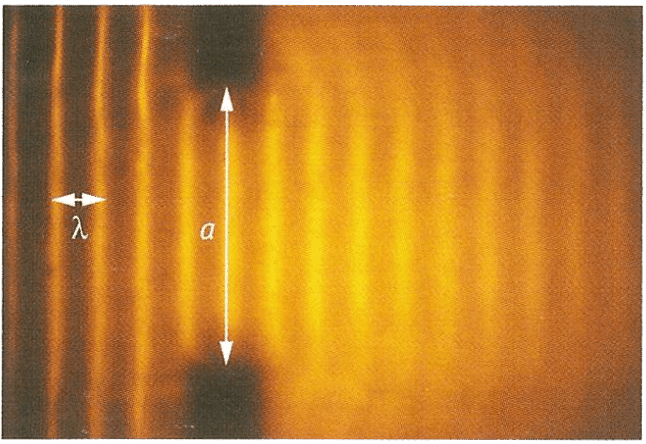


3 - Angle caractéristique de diffraction
a - Schéma
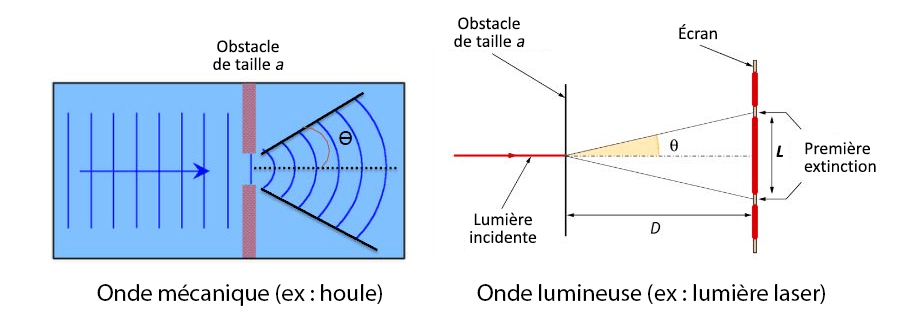
b - Relation
En notant a la taille de l’obstacle, \(λ\) la longueur d’onde et \(θ\) l’angle de diffraction, on a : \(θ = \dfrac{λ}{a}\).
Remarque : Dans le cas d'une figure de diffraction obtenue avec une onde lumineuse (schéma de droite ci-dessus), comme \(tan(\theta) = \dfrac{L/2}{D}\), en travaillant avec de petits angles, on obtient la relation : \(\dfrac{L}{2} = \dfrac{\lambda·D}{a}\).
c - Condition d’observation de la diffraction
- - si \(λ > a\), la diffraction est très importante, l’onde diffractée occupe tout l’espace qui lui est offert après l’obstacle
- - si \(λ ≤ a\), l’onde diffractée occupe une partie de l’espace avec la relation : \(θ = \dfrac{λ}{a}\).
- - remarque : si \(λ ≪ a\), alors \(θ = 0\), c'est-à-dire que l’onde se propage en ligne droite (pas de diffraction).
V - Interférences
1 - Mise en évidence
Lorsque deux ondes arrivent en un point, l’onde résultante s’obtient en faisant la somme des perturbations des deux ondes.
Considérons deux ondes de même fréquence qui se croisent :
- • Si les signaux sont en phase : l’amplitude augmente, on parle d’interférence constructive.
- • Si les signaux sont en opposition de phase : l’amplitude diminue : on parle d’interférence destructive.
Sur ostralo.net : croisement de deux ondes
En conséquence, dans certaines conditions :
- - lumière + lumière = obscurité
- - son + son = silence
- - vague + vague = mer plate
2 - Conditions d’interférences en général
8.A5 - Principe des interférences
Considérons deux ondes de même fréquence et émises en phase à partir de deux sources \(S_1\) et \(S_2\).
On s’intéresse à ce qu’il se passe en un point \(M\).
Notons \(d\) la différence de chemin parcouru par les ondes : \(d = S_2M - S_1M\).
⯈ Conditions d'interférences constructives
On observe des interférences constructives au point \(M\) si les deux ondes y arrivent en phase.
Autrement dit, si la différence de chemin parcouru est un multiple de \(λ\).
Soit encore si \(d = k·λ\) où \(k\) est un entier (positif, négatif ou nul).
⯈ Conditions d'interférences destructives
On observe des interférences destructives au point \(M\) si les deux ondes y arrivent en opposition de phase.
Autrement dit si la différence de chemin parcouru est un multiple de \(λ\) plus une \(½·λ\).
Soit encore, si \(d = (k+\dfrac{1}{2})·λ\) où \(k\) est un entier (positif, négatif ou nul).
3 - Cas des ondes lumineuses
a - Indice optique d’un milieu
L’indice d’un milieu est notée \(n\). C'est une grandeur sans unité. Par ailleurs \(n \geq 1\).
\(Célérité = \dfrac{Célérité\ dans\ le\ vide}{n}\) et \(Longueur\ d’onde = \dfrac{Longueur\ d’onde\ dans\ le\ vide}{n}\)
b - Chemin optique
On appelle chemin optique d’une onde lumineuse la grandeur \(δ = \dfrac{Distance}{n}\).
c - Conditions d’interférences
• En notant \(\delta\) la différence de chemin optique, les conditions d’interférences constructives deviennent : \(δ = k·λ_0\).
En effet, \(d = k·λ\). Soit \(d = k·λ_0·n\). Soit \(\dfrac{d}{n} = k·λ_0\). Soit \(δ = k·λ_0\).
• Les conditions d’interférences destructives deviennent, de même : \(δ = (k+\frac{1}{2})·λ_0\).
4 - Exemple des trous d’Young (ou des fentes d'Young)
a - Figure d’interférence avec des trous d’Young (ou des fentes d'Young)
Le dispositif expérimental pour les fentes d'Young est le même que celui utilisé en TP pour visualiser la diffraction, mais on remplace la fente simple par une fente double.

La figure obtenue à l'écran est la suivante :
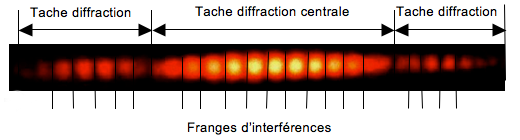
Sur ostralo.net : diffraction et interférences
b - Situation
Notations :
- - distance entre les trous \(S_1\) et \(S_2\) : \(b\)
- - distance entre les trous et l’écran : \(D\)
- - indice du milieu de propagation de l’onde : \(n\)
- - longueur d’onde dans le vide : \(λ_0\)
- - interfrange : \(i\)
Schéma :
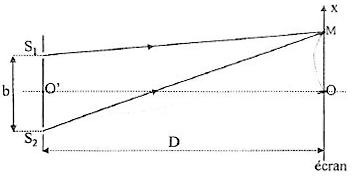
c - Différence de chemin optique
Pour un point \(M\) de l’écran, la différence de chemin optique est \(δ = S_2M – S_1M\)
Sur l’écran, on choisit un repère \(Ox\) tel que représenté sur le schéma.
Alors, si \(b \ll D\), on peut montrer que (formule qui sera donnée) : \(δ = n·b·\dfrac{x}{D}\). Soit aussi \(x = \dfrac{δ·D}{n·b}\)
d - Conditions d’interférences
Interférences constructives : \(δ = k·λ_0\).
Interférences destructives : \(δ = (k+\frac{1}{2})·λ_0\).
e - Formule de l’interfrange
\(i = x_{k+1} – x_k\)
Soit \(i = \dfrac{(k+1)·λ_0·D}{n·b} - \dfrac{k·λ_0·D}{n·b}\)
Soit \(i = \dfrac{λ_0·D}{n·b}\)