7.Eac3 : Vitesse volumique à partir d'un graphique

On s'intéresse à la réaction entre les ions argent \(\ce{Ag+}\) et le fer \(\ce{Fe}\) dont l'équation est : \(\ce{2 Ag+ (s) + Fe (s) -> Fe^2+ (aq) + 2 Ag (s)}\)

Le graphique donnant l'évolution de la concentration en \(\ce{Ag+}\) et en \(\ce{Fe^2+}\) est donné ci-dessous.

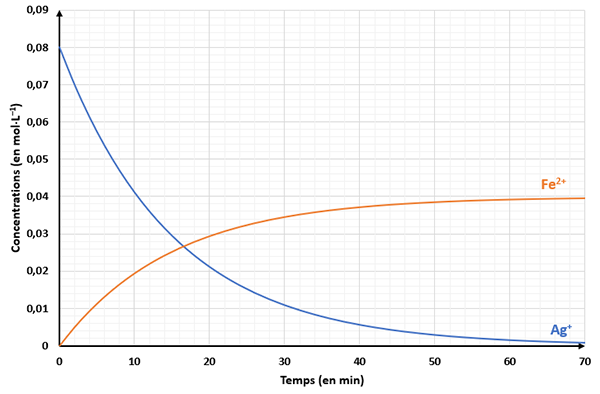
A partir du graphique :

1 Déterminer le temps de demi-réaction.

2 Déterminer la vitesse volumique d'apparition de \(\ce{Fe^2+}\) à l'instant initial.

3 Déterminer la vitesse volumique de disparition de \(\ce{Ag+}\) à l'instant initial.

4 Déterminer la vitesse volumique d'apparition de \(\ce{Fe^2+}\) au bout de \(\pu{20 min}\).

Afficher la correction

Graphiquement, on détermine que t_½ = 10 min.

La vitesse volumique d'apparition de \(\ce{Fe^2+}\) à l'instant initial est le coefficient directeur de la tangente à la courbe orange à l'origine.

Graphiquement, on obtient :

\(\begin{aligned}[t] v &= \dfrac{c_B - c_A}{t_B - t_A} \\ &= \dfrac{\pu{0,05} - 0}{20 - 0} \\ &= \pu{0,0025 mol*L-1*min-1} \end{aligned}\)

La vitesse volumique de disparition de \(\ce{Ag^+}\) à l'instant initial est l'opposé du coefficient directeur de la tangente à la courbe bleue à l'origine.

Graphiquement, on obtient :

\(\begin{aligned}[t] v &= -\dfrac{c_B - c_A}{t_B - t_A} \\ &= -\dfrac{\pu{0,026} - \pu{0,08}}{10 - 0} \\ &= \pu{0,0054 mol*L-1*min-1} \end{aligned}\)

La vitesse volumique d'apparition de \(\ce{Fe^2+}\) à \(t = \pu{20 min}\) est le coefficient directeur de la tangente à la courbe orange à cet instant.

Graphiquement, on obtient :

\(\begin{aligned}[t] v &= \dfrac{c_B - c_A}{t_B - t_A} \\ &= \dfrac{\pu{0,044} - \pu{0,016}}{40 - 0} \\ &= \pu{0,00070 mol*L-1*min-1} \end{aligned}\)