Chap06 : Mouvements dans un champ de gravitation

Animation pour visualiser les satellites présents autour de la Terre : Stuff In Space

Mouvement d'un satellite autour de la Terre : http://physique.ostralo.net/kepler/

I - Préambule

1 - Choix du référentiel

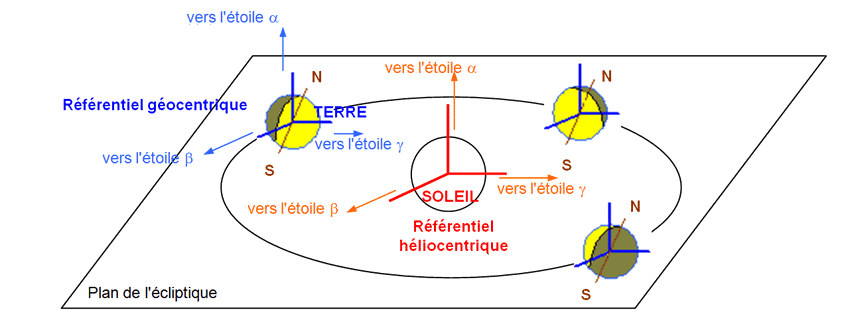
Référentiel héliocentrique : Solide imaginaire constitué du centre du Soleil et de trois directions vers des étoiles très éloignées.

Référentiel géocentrique : Solide imaginaire constitué du centre de la Terre et de trois directions vers trois étoiles très éloignées.

2 - Force de gravitation

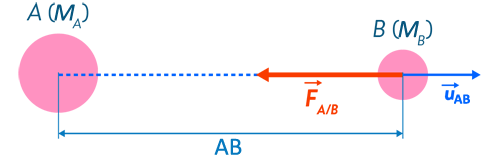
Expression vectorielle : loi universelle de la gravitation

Lorsqu'un objet B de masse \(M_B\) est placé une distance \(AB\) d'un objet A de masse \(M_A\), l'objet A exercice sur l'objet B une force gravitationnelle \(\overrightarrow{F_{A/B}}\)

\(\overrightarrow{F_{A/B}}=-G·\dfrac{M_A·M_B}{AB^2}·\overrightarrow{u_{AB}}\).

Où :

\(\overrightarrow{u_{AB}}\) est un vecteur unitaire orienté de A vers B.
\(AB\) la distance entre A et B (en m).
\(G\) est la constante universelle de gravitation, \(G = \pu{6,67E{–11} m^3·kg^{–1}·s^{–2}}\)
\(M_A\) et \(M_B\) les masses (en kg)

Expression pour les normes

Pour les normes, cette relation devient : \(F_{A/B}=G·\dfrac{M_A·M_B}{AB^2}\)

II - Lois de Kepler

Voir 6.TP1 - Lois de Kepler

Énoncé des trois lois de Kepler

Première loi (loi des orbites) : Les trajectoires des planètes sont des ellipses dont le Soleil occupe l’un des foyers.

Deuxième loi (loi des aires) : Si S est le Soleil et P la position d’une planète, le segment [SP] balaie des aires égales pendant des durées égales.

Troisième loi (loi des périodes) : Le carré de la période de révolution \(T\) d’une planète est proportionnel au cube du demi-grand axe \(a\) de sa trajectoire elliptique : \(\dfrac{T^2}{a^3}=cte\).

III - Mouvement circulaire autour d’un centre attracteur

1 - Présentation du problème

On considère une planète P de masse \(M_P\) qui tourne autour du Soleil S de masse \(M_S\).

Cas particulier étudié : La trajectoire de P autour de S est circulaire (cercle de rayon \(R = SP\)).

Objectifs :

- déterminer les coordonnées du vecteur accélération ;
- démontrer que la vitesse est constante et déterminer son expression ;
- établir la troisième toi de Kepler.

2 - Démonstration

Préambule

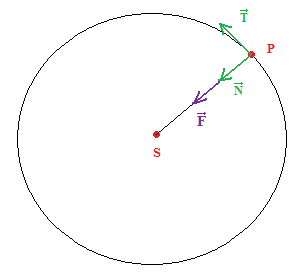
• Système : planète P

• Référentiel : héliocentrique considéré comme galiléen

• Repère de travail : repère de Frenet

• Bilan des forces : force de gravitation exercée par le Soleil, \(\vec{F}\), dirigée de la planète vers le Soleil.

Coordonnées de la force de gravitation

Comme le mouvement est circulaire, \(\vec{F}\) est suivant la normale est vers l’intérieur de la concavité.

\( \vec{F}~ \left|\begin{align} &F_T = 0 \\ &F_N = G·\dfrac{M_S·M_P}{SP^2} = G·\dfrac{M_S·M_P}{R^2} \end{align}\right.\)

Coordonnées du vecteur accélération

• 2^ème loi de Newton : \( \vec{F}=M_P·\vec{a}\) et donc \( \vec{a} = \dfrac{\vec{F}}{M_P} \)

• Coordonnées dans le repère de Serret-Frenet

\(\vec{a}~ \left|\begin{align} &a_T = \dfrac{F_T}{M_P} = \dfrac{0}{M_P} = 0 \\ &a_N = \dfrac{F_N}{M_P} = \dfrac{G·\dfrac{M_S·M_P}{R^2}}{M_P} = \dfrac{G·M_S}{R^2} \end{align}\right.\)

Valeur de la vitesse

On sait que, dans le repère de Frenet :

\(\vec{a}~ \left|\begin{align} &a_T = \dfrac{dv}{dt} \\ &a_N = \dfrac{v^2}{R} \end{align}\right.\)

• En raisonnement suivant la tangente :

On obtient \( \dfrac{dv}{dt} = 0 \). On en déduit que la vitesse constante.

• En raisonnement suivant la normale :

On obtient \(\dfrac{v^2}{R} = \dfrac{G·M_S}{R^2}\). On en déduit que \(v=\sqrt{\dfrac{G·M_S}{R}}\).

Troisième loi de Kepler

• Relation entre la période \(T\) et la vitesse \(v\) :

On raisonne sur 1 tour. Comme la vitesse est constante, \(v=\dfrac{d}{t}\). Soit \(v = \dfrac{2π×R}{T}\)

• 3^ème loi de Kepler

Les relations \(v = \sqrt{\dfrac{G·M_S}{R}}\) et \(v = \dfrac{2π×R}{T}\) permettent d'écrire \(\sqrt{\dfrac{G·M_S}{R}} = \dfrac{2π×R}{T}\).

Soit \(\dfrac{G·M_S}{R} = \dfrac{4π^2·R^2}{T^2}\). Soit \(\dfrac{R^3}{T^2} = \dfrac{G·M_S}{4\pi^2}\). On retrouve la 3^ème loi de Kepler.

• Remarque : expression de \(T\)

La relation précédente permet d'écrire \(T = 2π\sqrt{\dfrac{R^3}{G·M_S}} \).