5.E9 : Accélération d'une particule (aspect énergétique)

Un ion \(\ce{Mg^2+}\) est produit dans la chambre d'ionisation d'un spectromètre de masse.

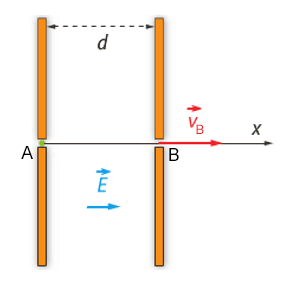
Cet ion, de masse \(m\), pénètre en position A, avec une vitesse initiale \(v_A\) de valeur négligeable, dans un champ électrique uniforme \(\vec{E}\) entre deux armatures planes parallèles distante de \(d\) d'un condensateur. Il est accéléré jusqu'à la position B où il atteint une vitesse de valeur \(v_B\).

On étudie le mouvement de cet ion assimilé à un corps ponctuel dans un référentiel terrestre considéré comme galiléen.

On néglige le poids de l'ion devant la force électrique à laquelle il est soumis entre les positions A et B du condensateur plan.

Données :

\(e = \pu{1,6E-19 C}\)

\(d = \pu{1,0 cm}\)

\(E = \pu{2,0E6 V*m-1}\)

\(v_B = \pu{5,6E5 m*s-1}\)

1 Exprimer la variation de l'énergie cinétique de l'ion \(\ce{Mg^2+}\) entre les positions A et B en fonction de \(m\) et \(v_B\).

2 Exprimer le travail de la force électrique subie par l'ion \(\ce{Mg^2+}\) entre les positions A et B en fonction de \(d\), \(e\) et \(E\).

3 Appliquer le théorème de l'énergie cinétique pour exprimer la masse de l'ion \(\ce{Mg^2+}\). La calculer.

Afficher la correction

\(\begin{aligned} Ec_B - Ec_A &= \frac{1}{2}~m~{v_B}^2 - \frac{1}{2}~m~{v_A}^2 \\ &= \frac{1}{2}~m~{v_B}^2 - 0 \\ &= \frac{1}{2}~m~{v_B}^2 \end{aligned}\)

\(\begin{aligned} W_{AB}(\vec{F_{alec}}) &= AB × F_{élec} × cos(angle) \\ &= AB × F_{élec} × cos(0) \\ &= AB × F_{élec} \\ \end{aligned}\)

Or \(AB = d\) et \(F_{élec} = 2e·E\)

Donc : \(W_{AB}(\vec{F_{élec}}) = d × (2~e~E)\)

D'après le théorème de l'énergie cinétique : \(Ec_B - Ec_A = \sum W_{AB}(\vec{Forces})\)

Donc : \(\frac{1}{2}~m~{v_B}^2 = d × (2~e~E)\)

Soit : \(m = \dfrac{2 × d × (2~e~E)}{{v_B}^2}\)

Application numérique :

\(\begin{aligned} m &= \dfrac{2 × (\pu{1,0E-2 m}) × 2 × (\pu{1,6E-16 C}) × (\pu{2,0E6 V*m-1})} {(\pu{5,6E5 m*s-1})^2} \\ &= \pu{4,1E-26 kg} \end{aligned}\)