5.E8 : Accélérateur de particules

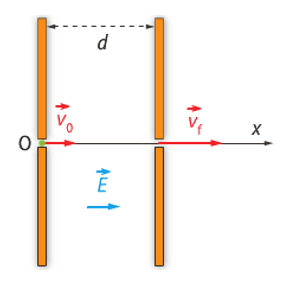
Dans un accélérateur linéaire de particules, un proton de charge e et de masse \(m = \pu{1,7E–27 kg}\) pénètre avec une vitesse initiale de valeur \(v_0 = \pu{2,0E3 m*s–1}\), perpendiculaire aux armatures d’un condensateur plan. Dans ce condensateur règne un champ électrostatique uniforme de valeur \(E = \pu{1,0 kV.m–1}\). Le poids du proton est négligé. Sa vitesse finale doit être \(v_f = 2~v_0\).

1.a Quelles sont les caractéristiques de la force \(\vec{F}\) subie par le proton ?

1.b Écrire la deuxième loi de Newton appliquée au proton. Projeter cette relation sur l’axe \((Ox)\) et établir une relation entre l’accélération \(a_x\), \(E\), \(m\) et \(e\).

2.a Quel est le mouvement du proton ?

2.b Justifier le nom d’accélérateur.

3 Le mouvement est étudié selon un axe horizontal \((Ox)\), orienté dans le sens du mouvement, dont l’origine coïncide avec la position d’entrée de la particule dans le condensateur. Déterminer les équations horaires de la vitesse \(v(t)\) et de la position \(x(t)\) du proton.

4.a A quel instant \(t_f\) le proton a-t-il atteint la vitesse \(v_f\) ?

4.b En déduire la distance \(d\) entre les deux armatures.

Afficher la correction

1a)

Le champ \(\vec{E}\) est horizontal vers la droite.

La particule est un proton, donc \(q = e\). Or \(\vec{F} = q~\vec{E}\). Alors \(\vec{F}\) est horizontale vers la gauche.

1.b)

D’après la deuxième loi de Newton, \(∑\overrightarrow{Forces} = m~\vec{a}\). Soit, ici : \(e~\vec{E} = m~\vec{a}\).

Soit, suivant l’axe Ox : \(e·E_x = m·a_x\). Or \(E_x=E\). D’où \(a_x = \dfrac{e·E}{m}\).

2.a)

Le vecteur accélération étant un vecteur constant et ayant le même sens que le vecteur vitesse, le mouvement est un mouvement rectiligne uniformément accéléré.

2.b)

« Accélérateur » sous-entend que la particule gagne de la vitesse, ce qui est bien le cas dans un mouvement uniformément accéléré.

3)

Pour la vitesse :

\(v_x(t) =\) primitive de \(a_x(t)\).

Soit \(a_x(t) = eE/m·t + {v_0}_x\).

Or \({v_0}_x = v_0\).

D’où \(v_x (t) = \dfrac{eE}{m}~t + v_0\).

Pour la position :

\(x(t) =\) primitive de \(v_x(t)\).

Soit \(x(t) = \dfrac{eE}{2·m}·t^2 + v_0·t + x_0\).

Or \(x_0 = 0\).

D’où \(x(t) = \dfrac{eE}{2m}~t^2 + v_0~t\).

4.a)

On a \(v_x(t_f) = v_f\) et \(v_x (t) = \dfrac{eE}{m}~t + v_0\).

D’où \(v_f = \dfrac{eE}{m}~t_f + v_0\).

Soit \(t_f = \dfrac{m}{eE}~(v_f-v_0)\).

Comme il faut que \(v_f = 2~v_0\), on obtient : \(t_f = \dfrac{m}{eE}~v_0\)

4.b)

\(\begin{align} d &= x(t_f) \\ &= \dfrac{eE}{2m}~t{_f}^2 + v_0 ~t_f \\ &= \dfrac{eE}{2m}~\left(\dfrac{m}{eE}~v_0\right)^2 + v_0~\left(\dfrac{m}{eE}~v_0\right) \\ &= \left(\dfrac{eE}{2m}\right) \left(\dfrac{m}{eE}\right)^2~{v_0}^2+\dfrac{m}{eE}~{v_0}^2 \\ &= \dfrac{m}{2eE}~{v_0}^2 + \dfrac{m}{eE}~{v_0}^2 \\ &= \dfrac{3m}{2eE}~{v_0}^2 \end{align}\)

\(\begin{align} d &= \dfrac{3×(\pu{1,7E–27 kg})}{2×(\pu{1,6E-19 C})~(\pu{1,0E3 V.m–1})}~(\pu{2,0E3 m*s–1})^2 \\ &= \pu{6,3E-5 m} \\ \end{align}\)