5.E4 : Saut en parachute

Le mouvement d’une parachutiste équipé de son parachute est étudié dans le référentiel terrestre. Le système {parachutiste + parachute} est assimilé à son centre de masse. La masse du système est \(m = \pu{110 kg}\). On supposera qu’il n’y a pas de vent et que la trajectoire est rigoureusement verticale.

La courbe ci-dessous représente l’évolution de la valeur de la vitesse du système en fonction du temps.

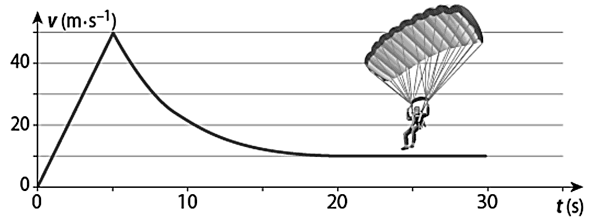
On choisit de travailler dans un repère à une dimension dont le vecteur unitaire \(\vec{j}\) est vertical et vers le bas.

1 Montrer que, comme le système étudié descend, on a égalité entre la valeur de la vitesse et la coordonnée du vecteur vitesse.

2 Première phase du saut.

2.a Au bout de combien de temps le parachutiste ouvre-t-il son parachute ?

2.b Déterminer l’expression \(v_1(t)\) de la vitesse pour la première phase du mouvement.

2.c En déduire l’expression \(a_1(t)\) de l’accélération.

2.d Quelle est la nature du mouvement du système pour cette première phase du saut.

2.e Que peut-on dire des forces qui s’exercent sur le système étudié ?

3 Troisième phase du saut : après \(\pu{20 s}\).

3.a Déterminer l’expression de \(v_3(t)\).

3.b En déduire la nature du mouvement du système étudié pour cette troisième phase du saut.

3.c Que peut-on en déduire quant aux forces qui s’exercent sur le système étudié ?

Afficher la correction

Comme le système descend, le vecteur vitesse est orienté vers le bas. Or, le repère choisi a un axe orienté vers le bas. Donc la coordonnées \(v_y(t)\) de la vitesse est égale à la vitesse \(v(t)\).

D’après le graphique, le parachutiste ouvre son parachute à t = 5 s car on observe une diminution brusque de la vitesse.

2.a

D’après le graphique, \(v_1(t)\) est une droite qui passe par l’origine du graphe. Soit \(v_1(t) = k·t\). Où \(k\) est le coefficient directeur.

Graphiquement on trouve \(k = \dfrac{\pu{50 m*s–1}}{\pu{5 s}} = \pu{10 m*s–2}\).

Et donc \(v_1(t) = 10~t\) avec \(t\) en \(s\) et \(v_1\) en \(\pu{m*s–1}\).

2.c

On sait que \(a_1(t)\) est la dérivée de \(v_1\).

D’où \(a_1(t) = \pu{10 m*s–2}\).

2.d

Comme l’accélération est constante et que la trajectoire est une droite, le mouvement est uniformément accéléré.

2.e

D’après la 2ème loi de Newton \(∑\overrightarrow{Forces} = m·\vec{a}\). Comme \(\vec{a}\) est un vecteur constant (cf. 2e)), alors \(∑\overrightarrow{Forces}\) est un vecteur contant.

Remarque : en fait ici, le système n’est soumis qu’à son poids,\(∑\overrightarrow{Forces} = \vec{P}\). On retrouve \(\vec{a} = \vec{g}\) soit \(a = g = \pu{10 m*s–2}\).

3.a

D’après le graphique \(v_3(t) = \pu{10 m*s–1}\).

3.b

Pour cette phase, le mouvement est rectiligne uniforme car la trajectoire est une droite et la vitesse est constante.

3.c

Comme le mouvement est rectiligne uniforme, alors \(\vec{a} = \vec{0}\).

Donc, d’après la deuxième loi de Newton, \(\sum{\overrightarrow{Forces}} = \vec{0}\)