Système : l'enseigne
Référentiel d'étude : le référentiel terrestre considéré comme galiléen
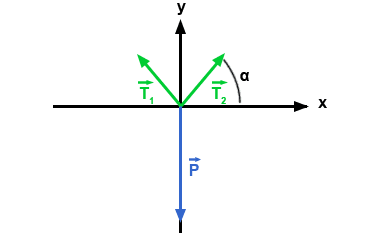
Bilan des forces : \(\vec{P}\), \(\vec{T_1}\), \(\vec{T_2}\)

Deuxième loi de Newton : ici on peux écrire : \(\vec{P} + \vec{T_1} + \vec{T_2} = \vec{0}\)
Repère de travail pour les forces :
Coordonnées des forces :
\(\vec{P}~
\left|\begin{align}
&P_x = 0 \\
&P_y = - m~g
\end{align}\right.\)
\(\vec{T_1}~
\left|\begin{align}
&{T_1}_x = -T_1 × cos(\alpha) \\
&{T_1}_y = T_1 × sin(\alpha)
\end{align}\right.\)
\(\vec{T_2}~
\left|\begin{align}
&{T_2}_x = T_2 × cos(\alpha) \\
&{T_2}_y = T_2 × sin(\alpha)
\end{align}\right.\)
Exploitation de la deuxième loi de Newton avec les coordonnées
La relation vectorielle devient :
\(
\left\{\begin{align}
&P_x + {T_1}_x + {T_2}_x = 0 \\
&P_y + {T_1}_y + {T_2}_y = 0
\end{align}\right.\)
D'où
\(
\left\{\begin{align}
&0 + -T_1 × cos(\alpha) + T_2 × cos(\alpha) = 0 \\
&-mg + T_2 × sin(\alpha) + T_2 × sin(\alpha) = 0
\end{align}\right.\)
La première équation donne :
\(T_1 × cos(\alpha) = T_2 × cos(\alpha)\)
Soit : \(T_1 = T_2\)
Dans la suite on va noter \(T\) la tension des cables (\(T = T_1 = T_2\))
La deuxième équation donne :
\(P = T×sin(\alpha) + T×sin(\alpha)\)
Soit : \(mg = 2×T×sin(\alpha)\)
Soit : \(T = \dfrac{mg}{2sin(\alpha)}\)
Finalement :
\(\begin{align}
T &= \dfrac{mg}{2sin(\alpha)} \\
&= \dfrac{(\pu{3,0E3}) × \pu{9,8}}{2×sin(\pu{40°})} \\
&= \pu{2,3E4 N}
\end{align}\)

