5.E10 : Rebond d'une balle (aspect énergétique)

On lance une balle assimilée à un point matériel de masse \(m = \pu{55 g}\) verticalement vers le sol, avec une vitesse initiale \(v_0\).

L'axe vertical orienté vers le haut a pour origine le sol.

On réalise la vidéo du mouvement, puis, à l'aide d'un logiciel adapté, on obtient les courbes ci-dessous.

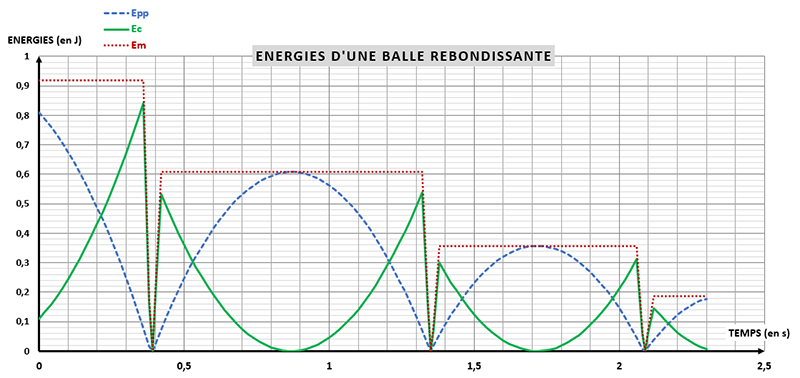
Donnée : \(g = \pu{9,81 N*kg-1}\)

1 Rappeler le nom et donner la définition des grandeurs \(Epp\), \(Ec\) et \(Em\).

2 Déterminer la valeur de la vitesse \(v_0\) avec laquelle la balle a été lancée.

3.a Indiquer le nombre de rebonds qui ont été filmés.

3.b Donner les dates de chacun des rebonds.

3.c Proposer une explication quand au fait que \(Ec\) s'annule à chaque rebond.

Dans cette question, on s'intéresse au mouvement de la balle entre le premier et le deuxième rebond.

4.a Justifier que les frottements peuvent être négligés.

4.b Déterminer la hauteur maximale atteinte par la balle.

4.c Représenter les allures des courbes \(Em\), \(Ec\) et \(Epp\) avec des frottements.

5 Justifier que la balle perd de l'énergie au cours de son mouvement et indiquer la cause de cette perte.

Afficher la correction

\(Epp\) est l'énergie potentielle de pesanteur. \(Epp = m·g·z\) avec un axe Oz vertical vers le haut.

\(Ec\) est l'énergie cinétique. \(Ec = \frac{1}{2}·m·v^2\).

\(Em\) est l'énergie mécanique. \(Em = Epp + Ec\).

\(Ec_0 = \frac{1}{2}·m·{v_0}^2\).

Donc \(v_0 = \sqrt{\dfrac{2·Ec_0}{m}}\)

Graphiquement, on détermine que \(Ec_0 = \pu{0,11 J}\)

Donc \(\begin{aligned}[t] v_0 &= \sqrt{\dfrac{2·Ec_0}{m}} \\ &= \sqrt{\dfrac{2 × (\pu{0,11 J})}{(\pu{0,055 kg})}} \\ &= \pu{2,0 m*s-1} \end{aligned}\)

3.a

Le nombre de rebonds est de trois.

3.b

Premier rebond à \(t_1 = 0,40 s\)

Deuxième rebond à \(t_2 = 1,35 s\)

Troisième rebond à \(t_3 = 2,08 s\)

3.c

L'énergie cinétique est liée à la vitesse. Donc si l'énergie cinétique s'annule, cela signifie qu'à chaque rebond la vitesse s'annule.

Or, à chaque rebond, le mouvement de la balle change de sens. Pour que cela soit possible, il faut que la vitesse s'annulle.

3.c

4.a

On observe que l'énergie mécanique est constante. Donc, d'après le théorème de la conservation de l'énergie, cela signifie que la balle n'est soumise qu'à son poids. Il n'y a donc pas de frottements.

4.b

\(Epp_{max} = m·g·z_{max}\)

Donc \(z_{max} = \dfrac{Epp_{max}}{m·g}\)

Or, graphiquement, on mesure que \(Epp_{max} = 0,60 J\)

Donc \(\begin{aligned}[t] z_{max} &= \dfrac{Epp_{max}}{m·g} \\ &= \dfrac{(\pu{0,60 J}))}{(\pu{0,055 kg})·(\pu{9,81 N*kg-1})} \\ &= \pu{1,1 m} \end{aligned}\)

4.c

On observe sur le graphique, qu'à chaque rebond, l'énergie mécanique passe d'un pallier à un autre, chaque nouveau palier étant à une valeur inférieure à celle du palier précédent.

Cette observation confirme une perte d'énergie de la balle.

Cette perte d'énergie est due au rebond.