4.E9 : Mouvement d'une locomotive

Dans le but de mettre en vente un nouveau modèle de locomotive pour train à grande vitesse, on fait subir à un prototype une série de tests.

Information : l’Union internationale des chemins de fer considère qu’un train roule à grande vitesse si sa vitesse dépasse \(\pu{200 km/h}\).

A - Démarrage de la locomotive

Dans un premier temps, on souhaite étudier le démarrage de la locomotive sur une portion de voie rectiligne horizontale.

Dans cette partie, on assimilera la locomotive à un point L et on travaillera dans un repère \((O, Ox)\).

Lors de ce test, on enregistre la vitesse du point \(L\) au cours du temps, ce qui permet d’obtenir le graphique ci-dessous. On admettra que l’abscisse \(v_x\) du vecteur vitesse est égale à la vitesse.

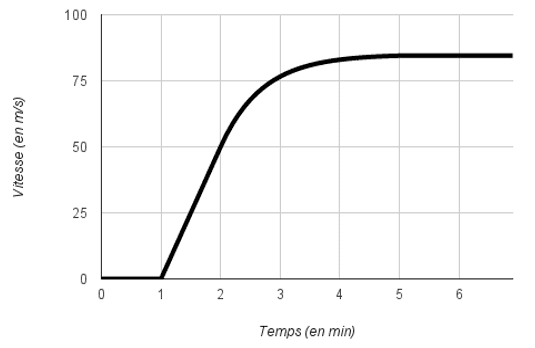
1 Quelle est la nature du mouvement de \(0\) à \(\pu{1 min}\) ?

2 On s’intéresse au mouvement de \(1\) à \(\pu{2 min}\).

3 Quelle est la nature du mouvement de \(2\) min à \(\pu{5 min}\) ?

4 On s’intéresse au mouvement au-delà de \(\pu{5 min}\).

B - Test des freins de la locomotive

La locomotive se déplace sur une portion de voie ferrée rectiligne horizontale. On assimilera la locomotive à un point \(L\). Le conducteur commence à freiner à l’instant \(\pu{t = 0 s}\) en un point \(O\) pris comme origine du repère de travail, et ce jusqu’à ce que la locomotive soit arrêtée. L’équation horaire du point \(L\) est alors \(x(t) = -0,30·t^2 + 50·t\) où \(x\) est en \(\pu{m}\) et \(t\) en \(\pu{s}\).

1 Donner les unités des deux valeurs numériques de l’équation horaire du point \(L\).

2 Établir l’expression de la coordonnée de la vitesse puis l’expression de la coordonnée de l’accélération.

3 Justifier à partir des résultats de la question précédente que le mouvement est rectiligne uniformément ralenti.

4 Quelle est la valeur de la vitesse de la locomotive à l’instant où le conducteur commence à freiner ?

5 On appelle \(t_{arrêt}\) le temps au bout duquel la locomotive s’arrête. Donner l’expression de \(t_{arrêt}\). Calculer \(t_{arrêt}\).

6 On appelle \(D_{arrêt}\) la distance au bout de laquelle la locomotive s’arrête. Calculer \(D_{arrêt}\).

C - Passage d’un virage

Un peu plus loin sur le trajet, un drone en vol stationnaire a permis de filmer le mouvement de la locomotive.

Dans cette partie, on assimilera la locomotive à un point \(L\).

Les positions successives du point \(L\) ont été reproduites sur la chronophotographie ci-dessous à intervalle de temps \(Δt = \pu{5 s}\).

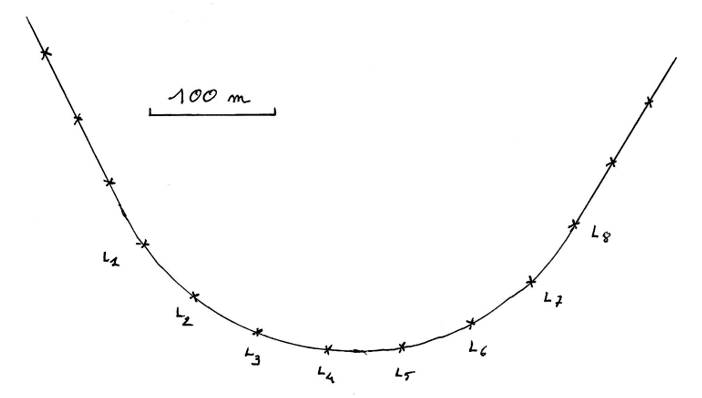
1 Quelle est la nature du mouvement sur cette portions de voie ferrée (de \(L_1\) à \(L_8\)) ?

2 Pour être aux normes, le tracé de la voie ferrée doit avoir un rayon supérieur à \(\pu{100 m}\). Cette condition est-elle vérifiée pour la portion de voie ferrée étudiée ?

3 Étude de la vitesse du train

4 Sans soucis d’échelle, tracer le vecteur accélération pour la position \(L_6\) du point \(L\).

Afficher la correction

A - Démarrage de la locomotive

1

Entre \(0\) et \(\pu{1 min}\), la vitesse est nulle, donc la locomotive est immobile.

2

2a

Entre \(1\) et \(\pu{2 min}\), la courbe peut être modélisée par une droite.

Donc \(v_x = k·t + b\). Soit, à partir de la courbe : \(v_x = 25·t – 50\) avec \(t\) en min et \(v_x\) en \(\pu{m/s}\).

2.b

ax est la dérivée de vx. Donc \(a_x = \pu{25 m*s–2}\).

2.c

Entre \(1\) et \(\pu{2 min}\), le mouvement est rectiligne uniformément accéléré.

3

Entre \(2\) et \(\pu{5 min}\), le mouvement est accéléré car la vitesse augmente.

4

4.a

On observe que la vitesse est constante. Donc le mouvement est rectiligne uniforme.

4.b

D’après le graphique, \(v = \pu{80 m/s} = \pu{2,9E2 km/h}\), ce qui est plus que \(\pu{200 km/h}\).

On peut donc affirmer que la locomotive roule à grande vitesse.

B - Test des freins de la locomotive

1

\(\pu{0,30}\) est en \(\pu{m*s–2}\) et \(\pu{50}\) en \(\pu{m*s–1}\).

2

La coordonnée \(v_x\) est la dérivée de \(x\). Donc \(v_x = –0,60·t + 50\).

La coordonnée \(a_x\) est la dérivée de \(v_x\). Donc \(a_x = \pu{–0,60 m*s–1}\).

3

La coordonnée \(a_x\) est négative donc le vecteur accélération est opposé au sens positif de l’axe.

En revanche, le vecteur vitesse est orienté dans le sens positif de l’axe car \(v_x(t=0) = \pu{50 m/s}\).

Donc le vecteur accélération est opposé au vecteur vitesse. Donc le mouvement est décéléré.

Comme par ailleurs la coordonnée \(a_x\) est constante et que le mouvement est rectiligne, on peut dire que le est uniformément décéléré.

4

\(v_x(t=0) = \pu{50 m/s}\).

5

On a \(v(t_{arrêt}) = 0\). D’où \(t_{arrêt} = \dfrac{50}{0,60} = \pu{83 s}\).

6

On a \(D_{arrêt} = x(t_{arrêt})\). Soit \(D_{arrêt} = −0,30·{t_{arrêt}}^2 + 50·t_{arrêt}\). Soit \(D_{arrêt} = \pu{2,0E3 m}\).

C - Passage d’un virage

1

D’après la chronophotographie, on peut affirmer que le mouvement est circulaire uniforme. Circulaire car la trajectoire est une portion de cercle. Uniforme que la locomotive parcourt des distances égales pendant des temps égaux.

2

Recherchons le centre du cercle par construction graphique en traçant les médiatrices des segments \([L_1L_3]\) et \([L_5L_7]\) (voir schéma en vert).

Mesurons le rayon. On trouve \(r_{papier} = \pu{6,4 cm}\). Soit \(r_{réel} = \pu{6,4} × \dfrac{100}{3} = \pu{2,1E2 m}\). Ce qui est bien supérieur à \(\pu{100 m}\).

2

3.a

\(v = \dfrac{d}{t}\). Soit ici, \(v = \dfrac{L_1L_2}{Δt}\). Or \({L_1L_2}_{papier} = \pu{3,4 cm}\). Soit \({L_1L_2}_{réel} = \pu{3,4} × \dfrac{100}{3} = \pu{1,1E2 m}\). D’où \(v = \pu{23 m*s–1}\).

3.b

Le vecteur vitesse est tangent à la trajectoire, dans le sens du mouvement, il aura \(\dfrac{23}{2} = \pu{11,5 cm}\) de long.

4

Comme le mouvement est circulaire uniforme, le vecteur accélération est perpendiculaire à la trajectoire vers le centre de la concavité (en rouge sur le schéma).