4.E8 : Mouvement d’une voiture

Une petite voiture télécommandée se déplace en ligne droite sur une table horizontale.

On travaille dans un repère \((O, Ox)\) orienté vers la droite.

On relève sa position \(x\) de son centre de masse au cours du temps.

Les résultats sont présentés dans le graphique ci-dessous.

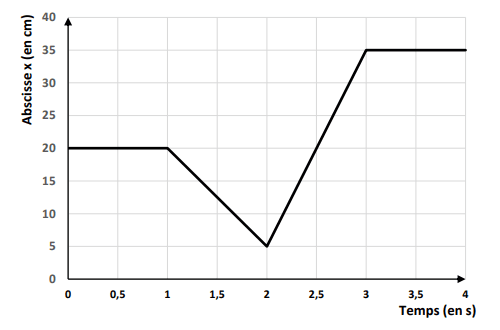
1 Entre \(\pu{0}\) et \(\pu{1 s}\)

1.a Quelle est la nature du mouvement du centre de masse entre \(\pu{0}\) et \(\pu{1 s}\) ? Justifier.

1.b En déduire la coordonnée \(v_x\) du vecteur vitesse.

2 Entre \(\pu{3}\) et \(\pu{4 s}\) ?

Reprendre les questions précédentes.

3 Entre \(\pu{1}\) et \(\pu{2 s}\)

3.a La voiture va-t-elle vers la gauche ou vers la droite ?

3.b A partir de la courbe, donner l’expression de \(x(t)\).

3.c En déduire l’expression de \(v_x(t)\).

3.d Quelle est la nature du mouvement ?

4 Entre \(\pu{2}\) et \(\pu{3 s}\)

Reprendre les questions précédentes.

5 Tracer la courbe donnant la coordonnée \(v_x\) du vecteur vitesse en fonction du temps.

Afficher la correction

Entre 0 et 1 s, le centre de masse de la voiture est immobile. En effet, d'après le graphique, son abscisse \(x\) est constante.

1.b

\(v_x\) est la dérivée de \(x(t)\).

Donc \(v_x = 0\).

On observe de même que l'abscisse \(x\) du centre de masse est constante. Donc il est immobile.

Comme précédemment, \(v_x = 0\).

3.a

Entre \(\pu{1}\) et \(\pu{2 s}\), \(x(t)\) diminue. Donc la voiture va dans le sens opposé au sens positif de l'axe : elle va vers la gauche.

3.b

D'après la courbe, \(x(t)\) est une droite.

On peut déterminer son équation :

Coefficient directeur : \(k = \dfrac{5-20}{2-1} = \pu{-15 cm*s-1}\)

Ordonnée à l'origine : \(b = \pu{35 cm}\)

Finalement : \(x(t) = -15~t + 35\)

3.c

\(\begin{align} v_x &= \dfrac{dx}{dt} \ &= \pu{-15 m*s-1} \end{align}\)

3.d

On vient de voir que \(v_x\) est constant. Donc le centre de masse de la voiture est animé d'un mouvement rectiligne uniforme.

Remarque : la coordonnée \(v_x\) étant négative, on retour le fait que la voiture va vers la gauche.

4.a

Entre \(\pu{2}\) et \(\pu{3 s}\), \(x(t)\) augmente. Donc la voiture va dans le sens positif de l'axe : elle va vers la droite.

4.b

D'après la courbe, \(x(t)\) est une droite.

On peut déterminer son équation :

Coefficient directeur : \(k = \dfrac{35-5}{3-2} = \pu{30 cm*s-1}\)

Ordonnée à l'origine : \(b = \pu{-55 cm}\)

Finalement : \(x(t) = 30~t - 55\)

4.c

\(\begin{align} v_x &= \dfrac{dx}{dt} \ &= \pu{30 m*s-1} \end{align}\)

4.d

On vient de voir que \(v_x\) est constant. Donc le centre de masse de la voiture est animé d'un mouvement rectiligne uniforme.

Remarque : la coordonnée \(v_x\) étant positive, on retour le fait que la voiture va vers la droite.