4.E7 : Équations horaires d’une chute libre

On étudie le mouvement d’un objet lâché depuis le troisième étage de la tour Eiffel, dont l’altitude au cours du temps est décrite par l’équation horaire suivante :

\(z(t) = -\frac{1}{2}·k·t^2+h_3\)

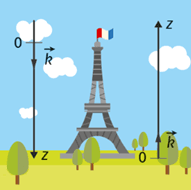
1 Des deux repères représentés sur la photo, identifier celui choisi pour la modélisation de la coordonnée \(z(t)\). Justifier.

2 Déterminer la durée de la chute jusqu’au sol.

3 Déterminer l’expression de la composante du vecteur vitesse \(v_z(t)\).

4 En déduire la valeur de la vitesse de l’objet au moment où il atteint le sol ?

5 Déterminer la valeur de la vitesse de l'objet au moment où il atteint le deuxième étage.

Données :

Hauteur du premier étage : \(h_1 = \pu{58 m}\)
Hauteur du deuxième étage : \(h_2 = \pu{116 m}\)
Hauteur du troisième étage : \(h_3 = \pu{276 m}\)
Coefficient : \(k = \pu{9,8 m*s–2}\)

Afficher la correction

Plusieurs arguments sont possibles pour affirmer que c'est le repère de droite (celui qui est orienté vers le haut) qui correspond à l'équation.

• A \(t = 0\), l'objet est au troisième étage, \(z(t = 0) = h_3\). Or il n'y a que dans le repère de droite que cela est correct.

• D'après l'équation, quand \(t\) augmente, \(z\) diminue. Cette propriété n'est correcte que dans le repère de droite.

Notons \(t_{sol}\) la durée de la chute.

Lorsque l'objet est au sol, \(z = 0\).

Donc \(z(t_{sol}) = 0\).

Donc \(-\frac{1}{2}·k·t_{sol}^2+h_3 = 0\).

Donc \(\frac{1}{2}·k·t_{sol}^2 = h_3\)

\(t_{sol}^2 = \dfrac{2·h_3}{k}\)

\(t_{sol} = \sqrt{\dfrac{2·h_3}{k}}\)

\(t_{sol} = \sqrt{\dfrac{2 × \pu{276 m}}{\pu{9,8 m*s^-2}}}\)

\(t_{sol} =\pu{7,5 s}\)

\(\begin{align} v_z(t) &= \dfrac{dz(t)}{dt} \\ &= -k·t \end{align}\)

\(\begin{align} v_{sol} &= v_z(t_{sol}) \\ &= -k·t_{sol} \\ &= - \pu{9,8} × \pu{7,5} \\ &= \pu{73,5 m*s-1} \end{align}\)

• Exprimons le temps mis pour atteindre le deuxième étage.

Donc \(z(t_2) = h_2\).

Donc \(-\frac{1}{2}·k·{t_2}^2+h_3 = h_2\).

Donc \(\frac{1}{2}·k·{t_2}^2 = h_3 - h_2\)

\({t_2}^2 = \dfrac{2·(h_3 - h_2)}{k}\)

\(t_2 = \sqrt{\dfrac{2·(h_3 - h_2)}{k}}\)

• Exprimons la vitesse à l'instant \(t_2\)

\(\begin{align} v_z(t_2) &= -k·t_2 \\ &= -k·\sqrt{\dfrac{2·(h_3 - h_2)}{k}} \\ &= -\sqrt{2·k·(h_3 - h_2)} \\ \end{align}\)

• Exprimons puis calculons \(v\)

\(\begin{align} v(t_2) &= \lvert v_z(t_2)\rvert \\ &= \sqrt{2·k·(h_3 - h_2)} \\ &= \pu{56 m*s-1} \end{align}\)