4.E3 : Analyse de graphiques

On considère un point animé d’un mouvement rectiligne uniforme.

On travail dans un repère à une dimension.

1 Attribuer les trois graphes ci-dessous aux grandeurs suivantes : position \(x(t)\), vitesse \(v_x(t)\) et de l’accélération \(a_x(t)\).

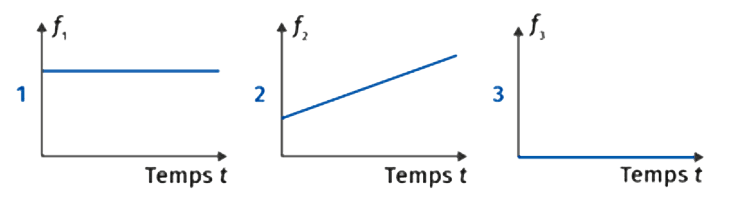
2 Dans quel sens de l’axe \(Ox\) le point se déplace-t-il ?

Afficher la correction

Le point étant animé d'un mouvement rectiligne uniforme.

On peut affirmer que \(v_x(t)\) ne dépend pas du temps, c'est à dire que \(v_x(t)\) est constant. Donc \(v_x(t)\) est \(f_1\).

Par ailleurs, \(a_x(t)\) est la dérivée \(v_x(t)\). Donc \(a_x(t) = 0\). Donc \(a_x(t)\) est \(f_3\).

Finalement \(x(t)\) est \(f_2\).

On observer sur la courbe \(f_2\), c'est-à-dire \x(t)\), que \x(t)\) augmente. Donc le point se déplace dans le sens positif de l'axe \(Ox\).