Chap04 : Décrire un mouvement
I - Référentiel et repères de travail
1) Référentiel
Un référentiel est un objet réel ou virtuel pris comme référence.
Pour l’étude des objets qui nous entourent, on travaille en général dans le référentiel terrestre.
2) Repère d’espace
Le repère d’espace est défini par une origine est des axes.
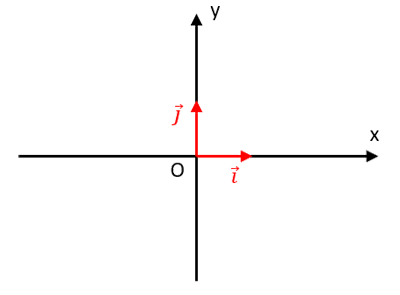
Suivant les situations, on choisit :
- - un repère à une dimension \((O,\ Ox)\) ou \((O,\ \overrightarrow{i})\)
- - un repère à deux \((O,\ Ox,\ Oy)\) ou \((O,\ \overrightarrow{i},\ \overrightarrow{j})\)
- - un repère à trois dimensions…
3) Repère de temps
Afin de se repérer dans le temps, il faut choisir une origine du temps.
II - Vecteur position
1) Vecteur position
Le vecteur position permet de connaitre à chaque instant la position du point M étudié.
Formules : \(\overrightarrow{OM}(t) = x(t)·\overrightarrow{i} + y(t)·\overrightarrow{j} + z(t)·\overrightarrow{j}\)
Cordonnées : \(\overrightarrow{OM}(t) \left| \begin{array}{1} x(t) \\ y(t) \\ z(t) \end{array} \right.\)
Vocabulaire : les coordonnées sont appelées les équations horaires.
Remarque : les coordonnées du vecteur position sont les mêmes que les coordonnées du point M.
2)Trajectoire
La trajectoire est la courbe obtenue à partir des positions successives du point M étudié.
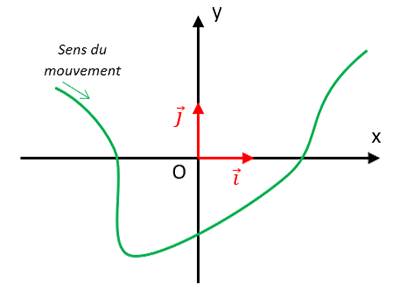
L’équation de la trajectoire se déduit des équations horaires en « éliminant \(t\) ».
III - Vecteur vitesse
1) Caractéristiques du vecteur vitesse
Le vecteur vitesse d'un point donne des informations sur la variation de la position de ce point.
Le vecteur vitesse \(\overrightarrow{v}\) a les caractéristiques suivantes :
- - direction : tangente à la trajectoire
- - sens : celui du mouvement
- - intensité : valeur de la vitesse (en \(\pu{m*s^–1}\)).
Remarque : on a l’habitude de représenter le vecteur vitesse avec son origine au point étudié.
Attention : la représentation des vecteurs vitesse nécessite une échelle spécifique.
2) Coordonnées du vecteur vitesse
Les coordonnées du vecteur vitesse sont \(v_x(t)\) et \(v_y(t)\). Elles s’expriment en \(\pu{m*s^–1}\).
3) Relation entre le vecteur position et le vecteur vitesse
4.Poly1 – Position ➢ Vitesse ➢ Accélération
Le vecteur vitesse est la dérivée du vecteur position.
Relations pour les coordonnées : \(\begin{aligned}[t] v_x(t)=\dfrac{dx(t)}{dt} \\ v_y(t) = \dfrac{dy(t)}{dt} \end{aligned}\)
IV - Vecteur accélération
1) Définition
Le vecteur accélération permet d’avoir des informations sur la façon dont le vecteur vitesse varie.
On le note \(\overrightarrow{a}\) ou \(\overrightarrow{a}(t)\). Son intensité s’exprime en \(\pu{m*s^–2}\).
Les coordonnées du vecteur accélération sont \(a_x(t)\) et \(a_y(t)\)
2) Lien entre le vecteur accélération et le vecteur vitesse
4.Poly1 – Position ➢ Vitesse ➢ Accélération
Le vecteur accélération est la dérivée du vecteur vitesse.
Relations pour les coordonnées : \(\begin{aligned}[t] a_x(t) = \dfrac{dv_x(t)}{dt} \\ a_y(t) = \dfrac{dv_y(t)}{dt} \end{aligned}\).
V - Cas particulier des mouvements circulaires
4.Poly2 - Repère de Frenet pour les mouvements circulaires
Repère de Frenet
On considère ici un point dont la trajectoire est une portion de cercle de rayon R.
Dans ce cas, on utilise un repère de travail particulier appelé le repère de Frenet.
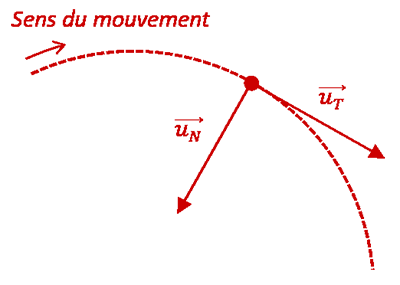
Ce repère a les caractéristiques suivantes :
- - origine O : le point étudié
- - vecteur unitaire \(\overrightarrow{u_T}\) : perpendiculaire à la trajectoire (donc porté par le rayon) et dirigé vers l’intérieur de la concavité ;
- - vecteur unitaire \(\overrightarrow{u_N}\) : parallèle à la trajectoire et dirigé dans le sens du mouvement.
Coordonnées du vecteur vitesse dans le repère de Frenet
\(\overrightarrow{v}(t) \left| \begin{array}{1} v_T = v \\ v_N = 0 \\ \end{array} \right.\)
Coordonnées du vecteur accélération dans le repère de Frenet
\(\overrightarrow{a}(t) \left| \begin{array}{1} a_T = \dfrac{dv}{dt} \\ v_N = \dfrac{v^2}{R} \\ \end{array} \right.\)