4.A2 : Mouvement circulaire : la centrifugeuse
Documents
Le g
Le \(\pu{G}\) (« G » étant l'initiale de « gravité ») est une unité d'accélération correspondant approximativement à l'accélération que subit un objet du fait de l’attraction de la Terre : \(\text{1-G} = \pu{9,80665 m*s-2}\). Par exemple, un objet qui tombe subit une accélération de \(\text{1-G}\).
Lors de certains mouvements (avec accélération, décélération ou de rotation), il est possible de ressentir une « force » importante. Il s’agit en fait d’une accélération. Pour quantifier cette accélération, on la comparer à celle que subit un objet en train de tomber.
Subir une accélération de \(\text{3-G}\) signifie que l’on a l’impression de peser 3 fois son poids habituel.
C’est ce phénomène qui est à l’origine des sensations que l’on ressent dans un manège d’une fête foraine.
La centrifugeuse

Lors de leur préparation, les astronautes ou les pilotes de chasse doivent s’entrainer à subir de fortes accélérations ou décélérations pour se préparer aux phases de décollage et d’atterrissage.
L’un des appareils utilisé pour cet entrainement est la centrifugeuse. Il s’agit d’un siège placé au bout d’un bras mécanique, l’ensemble tournant à grande vitesse.
Vidéo : https://www.dailymotion.com/video/x2rndoo
Une situation concrète
On considère une centrifugeuse dont le bras à une longueur \(L = \pu{6 m}\).
On notera \(P\) le point correspondant au centre de masse de la personne qui se place dans la nacelle de la centrifugeuse.
Lors d’un entrainement, un opérateur fait tourner la centrifugeuse avec une vitesse angulaire \(ω\) (la vitesse angulaire est le nombre de tour par seconde) dont l’évolution est donnée par le graphique ci-dessous.

On distingue trois phases :
- - phase 1 : de \(\pu{10 s}\) à \(\pu{20 s}\)
- - phase 2 : de \(\pu{20 s}\) à \(\pu{30 s}\)
- - phase 3 : de \(\pu{30 s}\) à \(\pu{40 s}\).
Questions
1 Dans quel référentiel le point \(P\) est-il immobile ? Dans quel référentiel sa trajectoire est-elle circulaire ?
2 Justifier que pour un point dont la trajectoire est circulaire on a : \(v=2πRω\) où \(v\) et la vitesse en \(\pu{m·s–1}\), \(R\) le rayon de la trajectoire en \(\pu{m}\) et \(ω\) la vitesse angulaire en \(\pu{tr·s–1}\) (tour par seconde).
3 Rappeler les expressions des coordonnées du vecteur vitesse et du vecteur accélération dans le repère de Frenet \((P,\vec{T},\vec{N})\) dans le cas général.
4 Étude de la phase 2
4.1 Quelle est la nature du mouvement de \(N\) pendant cette phase ?
4.2 Calculer les coordonnées du vecteur vitesse et du vecteur accélération pendant cette phase.
4.3 Représenter ces deux vecteurs sur le schéma ci-après à l’instant \(t = \pu{25 s}\).
4.4 Combien de \(\pu{G}\) subit la personne qui est dans la centrifugeuse lors de la phase 2 ?
5 Étude de la phase 1
5.1 A partir du graphique, donner l’expression de la vitesse angulaire en fonction du temps \(ω(t)\).
5.2 En déduire l’expression de la vitesse en fonction du temps \(v(t)\).
5.3 En déduire les expressions des coordonnées \(a_T(t)\) et \(a_N(t)\) du vecteur accélération dans le repère de Frenet en fonction du temps.
5.4 Calculer les valeurs des coordonnées du vecteur accélération et du vecteur vitesse à l’instant \(t = \pu{15 s}\).
5.5 Représenter ces deux vecteurs à l’instant \(t = \pu{15 s}\).
6 Étude de la phase 3
Reprendre les questions précédentes (de 5.1 à 5.5) à l’instant \(t = \pu{35 s}\).
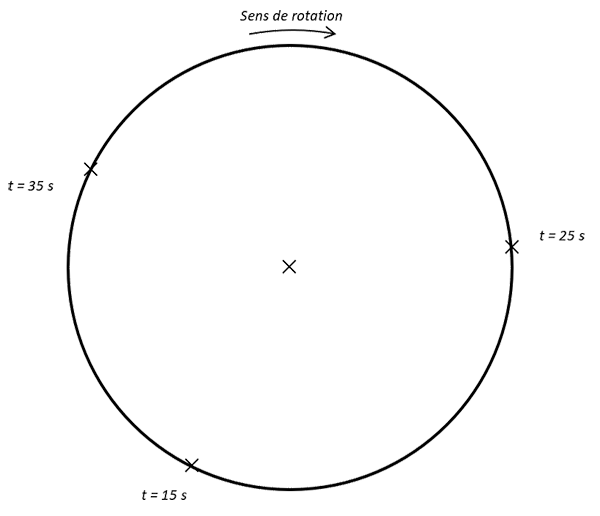
Positions du point \(P\) aux instant \(t = \pu{15 s}\), \(t = \pu{25 s}\) et \(t = \pu{35 s}\).