3.E6 : Dosage d’un sérum physiologique

Le sérum physiologique est une solution dont la composition est proche de celle du sérum sanguin. Il contient \(\pu{0,9 \%}\) en masse de chlorure de sodium \(\ce{(Na+(aq) ; Cl-(aq))}\), avec \(d = \pu{1,00}\). Il est utilisé à des fins médicales pour nettoyer les plaies, les yeux, faire une injection de médicaments en intraveineuse.

On souhaite vérifier la concentration d’un sérum physiologique noté \(S\) par conductimétrie.

Pour cela, on prélève \(V = \pu{10,0 mL}\) de \(S\) que l'on transvase dans un bécher. On y ajoute environ \(\pu{90 mL}\) d'eau distillée pour que la sonde de conductimétrie soit totalement immergée.

On dose les ions chlorure présents dans le bécher par une solution \(S'\) de nitrate d’argent \(\ce{(Ag+(aq) ; NO3-(aq))}\) de concentration \(c' = \pu{0,100 mol*L-1}\). Il se forme un précipité de chlorure d’argent \(\ce{AgCl (s)}\).

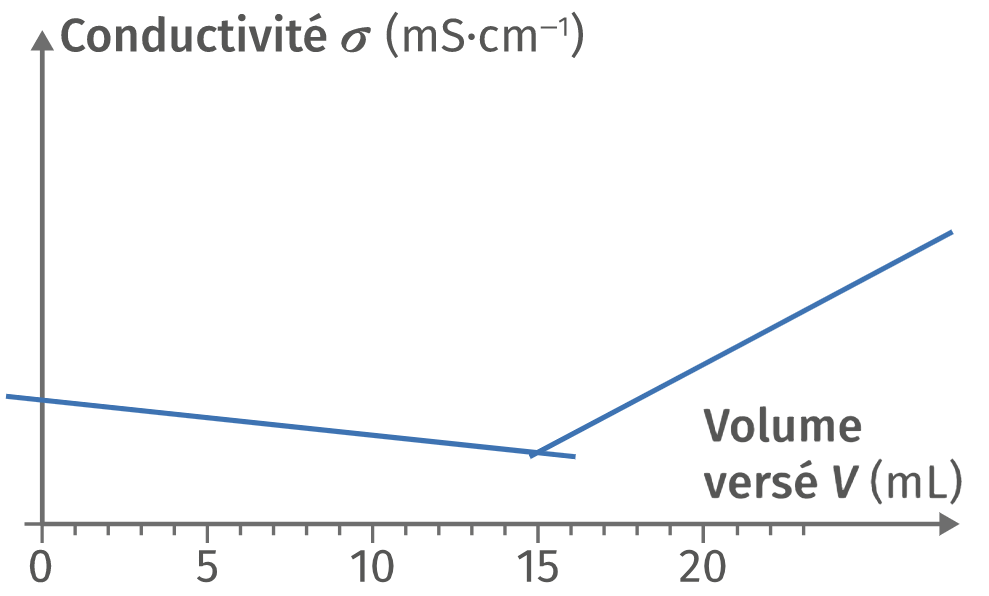
On relève la valeur de la conductivité après chaque ajout de solution titrante. La courbe \(σ = f(V)\) est tracée ci-dessous.

1 Écrire l’équation de la réaction support du dosage.

2 Déterminer le volume à l'équivalence.

3 En déduire la concentration en ions chlorure de la solution \(S\).

4 Comparer ce résultat avec les données d'une solution correspondant à un sérum physiologique.

5 Justifier qualitativement l’évolution de la pente de la courbe.

Données :

• Masse molaire du chlorure de sodium : \(M = \pu{58,5 g*mol–1}\).
• Conductivité molaires ioniques :

\(λ(\ce{Ag+}) = \pu{6,19 mS*m2*mol–1 }\);
\(λ(\ce{NO3–}) = \pu{7,14 mS*m2*mol–1 }\);
\(λ(\ce{Cl–}) = \pu{7,63 mS*m2*mol–1 }\);
\(λ(\ce{Na+}) = \pu{5,01 mS*m2*mol–1 }\);

Afficher la correction

L’équation de la réaction s’écrit : \(\ce{Ag+(aq)+Cl−(aq)→AgCl(s)}\)

D'après la courbe, en prenant l'abscisse de l'intersection des deux droites, on trouve que le volume à l'équivalence est \(V_E = \pu{15,2 mL}\).

À l’équivalence, on peut écrire : \(\dfrac{n(\ce{Cl-})}{1} = n_E(\dfrac{\ce{Ag+})}{1}\).

Soit \(c·V = c'·V_E\)

Et donc \(\begin{aligned}[t] c &= \dfrac{c'·V_E}{V} \\ &= \dfrac{(\pu{0,100 mol*L-1})×(\pu{15,2 mL})}{(\pu{10 mL})} \\ &= \pu{0,152 mol*L-1} \end{aligned}\)

On va calculer le pourcentage massique \(P_m\) de chlorure de sodium à partir de la concentration.

\(P_m = \dfrac{Masse\ de\ \ce{NaCl}\ dans\ un\ volume\ V\ de\ sérum}{Masse\ du\ volume \ V\ de\ sérum}\)

Or :

\(\begin{aligned}[t] Masse\ de\ \ce{NaCl}\ dans\ un\ volume\ V\ de\ sérum &= n × M \\ &= c × V × M \end{aligned}\)

\(\begin{aligned}[t] Masse\ du\ volume \ V\ de\ sérum &= V × \rho_{sérum} \\ &= V × d_{sérum} × \rho_{eau} \end{aligned}\)

Finalement \(\begin{aligned}[t] P_m &= \dfrac{c× V × M}{V × d_{sérum} × \rho_{eau}} \\ &= \dfrac{c × M}{d_{sérum} × \rho_{eau}} \\ &= \dfrac{(\pu{0,152 mol*L-1})×(\pu{58,5 g*mol-1})}{(\pu{1,00})×(\pu{1,00E3 g*L-1})} \\ &= \pu{8,89E-3} \\ &= \pu{0,889 \%} \end{aligned}\)

On retrouve la valeur attendue.

Avant l’équivalence, les ions chlorure sont « remplacés » par des ions nitrate, dont la conductivité molaire ionique est quasiment identique.

Après l’équivalence, toutes les concentrations en ions augmentent : la conductivité augmente.