3.E5 : Solubilité de l’acide benzoïque

L’acide benzoïque, de formule brute \(\ce{C6H5COOH}\), est un additif alimentaire connu sous le nom E210. On le rencontre notamment dans les jus de fruits.

On souhaite vérifier la solubilité de l’acide benzoïque dans l’eau, en réalisant un dosage avec suivi pH‑métrique. On dose \(V_A = \pu{20,0 mL}\) d’une solution d’acide benzoïque saturée à la concentration \(c_A\) par de la soude \(\ce{(Na+(aq)}\ ;\ \ce{HO–(aq))}\) de concentration \(c_B = \pu{5,00E−2 mol*L-1}\). On relève le \(pH\) pour chaque ajout de solution titrante. La courbe \(pH = f(V_B)\) est représentée ci‑dessous.

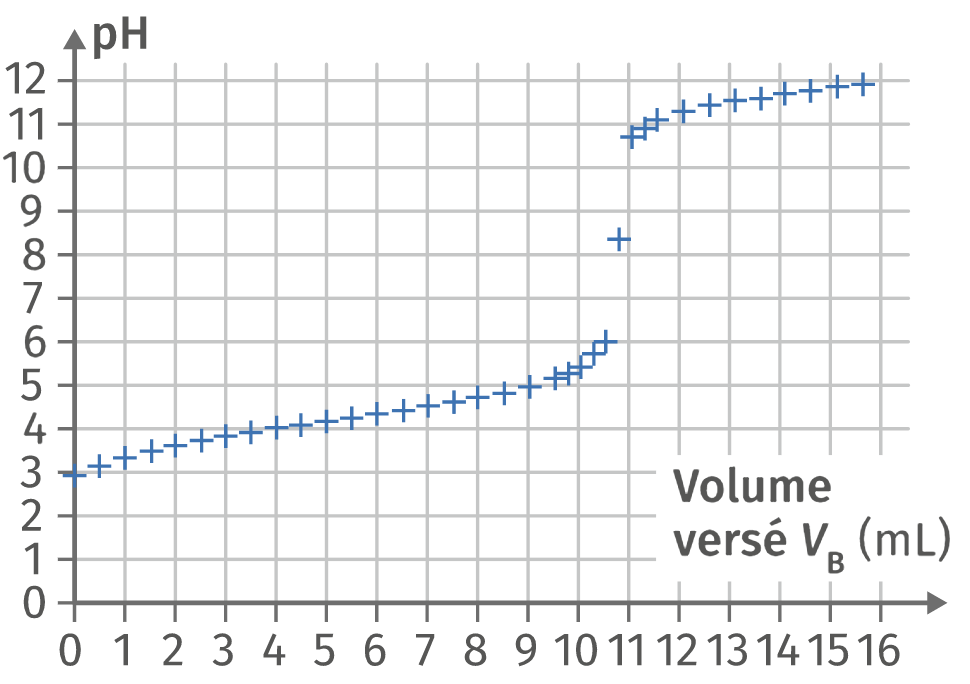
1 Écrire l’équation de la réaction support du dosage.

2 Déterminer le volume à l'équivalence.

3 En déduire la concentration en quantité de matière en acide benzoïque \(c_A\) dans la solution saturée.

4 Comparer ce résultat avec les données.

Données :

• Solubilité à \(\pu{24 °C}\) de l'acide benzoïque dans l'eau : \(s = \pu{3,26 g*L–1}\).
• Masse molaire de l'acide benzoïque : \(M = \pu{122,0 g*mol–1}\).
• Couples acide-base : \(\ce{C6H5COOH (aq)} / \ce{C6H5COO– (aq)}\).

Afficher la correction

L’équation de la réaction support du dosage s’écrit : \(\ce{C6H5COOH(aq) + HO^−(aq) -> C6H5COO−(aq) + H2O(l)}\)

Le volume à l'équivalence est déterminé à l’aide de la méthode des tangentes parallèles. Quand la courbe présente une symétrie, on peut tracer deux tangentes à la courbe, parallèles, de part et d’autre du saut de \(pH\), puis une droite, parallèle et équidistante aux deux autres.

Le point d’intersection de cette troisième droite avec la courbe a pour abscisse \(V_E = \pu{10,8 mL}\).

À l’équivalence, on peut écrire : \(n(\ce{C6H5COOH}) = n_E(\ce{HO−})\)

Soit : \(c_A · V = c_B · V_E\)

D'où : \(\begin{aligned}[t] c_A &= \dfrac{c_B·V_E}{V} \\ &= \dfrac{(\pu{5,00E−2 mol*L-1})×(\pu{10,8 mL})}{(\pu{20,0 mL})} \\ &= \pu{2,70E-2 mol*L-1} \end{aligned}\)

La solubilité d'une espèce est sa concentration en masse dans une solution saturée.

Or : \(c_m = c × M\)

D'où : \(\begin{aligned}[t] s_{exp} &= c_A × M \\ &= (\pu{2,70E-2 mol*L-1}) × (\pu{122,0 g*mol-1}) \\ &= \pu{3,29 g*L-1} \end{aligned}\)