Chap03 : Titrages pH-métriques et conductimétriques
I - Concentrations et pourcentage massique
3.A3 : Pourcentage massique et concentration
1) Définitions
a) Masse volumique
La masse volumique se note \(ρ\). Elle s'exprime en \(\pu{kg*m^-3}\) dans le système international, mais souvent en \(\pu{g*L-1}\) ou \(\pu{g*cm^-3}\) en chimie.
La masse volumique est donnée par la relation : \(ρ = \dfrac{m}{V}\) où \(m\) est la masse (masse totale) et \(V\) le volume.
b) Densité
La densité d'un fluide est donnée par la relation : \(d = \dfrac{ρ}{ρ_{eau}}\) où les masses volumiques ont la même unité.
Rappel : \(ρ_{eau} = \pu{10^3 kg*m^-3} = \pu{1 kg*L-1} = \pu{10^3 g*L-1}\).
c) Pourcentage massique (parfois appelé titre massique)
Le pourcentage massique d'une espèce chimique dans un mélange est donné par la relation suivante :
\(P_m = \dfrac{m_{espèce\ chimique\ en\ solution}}{m_{solution}}\) où les masses sont exprimées dans la même unité.
2) Concentration en masse ou en quantité de matière
a) Calcul de la concentration en masse
La connaissance de \(d\) et de \(P_m\) permet de calculer la concentration en masse \(C_m\).
Formule : \(C_m = P_m × d × ρ_{eau}\).
b) Calcul de la concentration en quantité de matière
La connaissance de \(d\), \(Pm\) et \(M\) permet de calculer la concentration en quantité de matière \(C\).
Formule : \(C = \dfrac{P_m × d × ρ_{eau}}{M}\).
II - Rappels sur les transformations chimiques
1) Vocabulaire
• Réactif : espèce chimique transformée par la réaction chimique.
• Produit : espèce chimique produite lors de la réaction chimique.
• Equation de la réaction chimique : \(\ce{réactif1 + réactif2 + ... -> produit1 + produit2 + ...}\)
• Fin d'une transformation chimique, état maximal : une transformation chimique atteint son état maximal lorsqu'au moins l'un des réactifs est entièrement consommé.
• Réactif en défaut (ou réactif limitant) : les réactifs en défaut sont ceux qui sont entièrement consommés dans l'état maximal. Il n'y a plus de réactif en défaut dans l'état maximal.
• Réactif en excès : les réactifs en excès sont ceux qui ne sont pas entièrement consommées dans l'état maximal. Il reste des réactifs en excès dans l'état maximal.
• Proportions stœchiométriques : les réactifs sont utilisés dans les proportions stœchiométriques lorsqu'ils sont entièrement consommées dans l'état maximal.
2) Avancement et tableaux d'avancement
III - Titrage
3.TP1 - Titrages directs pH-métriques
1) Principe général
a) Dispositif

b) Principe et vocabulaire
La solution dont on souhaite déterminer la concentration est appelée la solution titrée, elle contient le réactif titré.
La solution de concentration connue est la solution titrante, elle contient le réactif titrant.
Le titrage s’appuie sur une réaction chimique, souvent appelée réaction support du dosage, entre le réactif titré et le réactif titrant.
La solution titrante est versée progressivement, à l’aide d’une burette, dans le bécher contenant le réactif titré.
2) L’équivalence
a) Définition
L’équivalence correspond au moment où l’on a introduit l’espèce chimique titrante en proportion stœchiométrique avec l’espèce chimique titrée.
b) Relation entre les quantités de matières à l'équivalence

Considérons un titrage pour lequel :
- - l'espèce chimique titrante est notée \(A\) ;
- - l'espèce chimique titrée est notée \(B\) ;
- - l'équation de la réaction support du dosage est : \(\ce{aA + bB -> ...}\)
On note :
- • \(V_{B}\) le volume de solution titrée utilisé.
- • \(n(B)\) la quantité de matière de B présente dans le bécher ;
- • \(n_E(A)\) la quantité de matière de A versée à l'équivalence.
Alors : \(\dfrac{n_E(A)}{a} = \dfrac{n(B)}{b}\)
Ou également : \(\dfrac{C_A × V_E}{a} = \dfrac{C_B ×V_{B}}{b}\)
Remarque : Ces relations se démontrent facilement à l'aide du tableau d'avancement à l'équivalence.
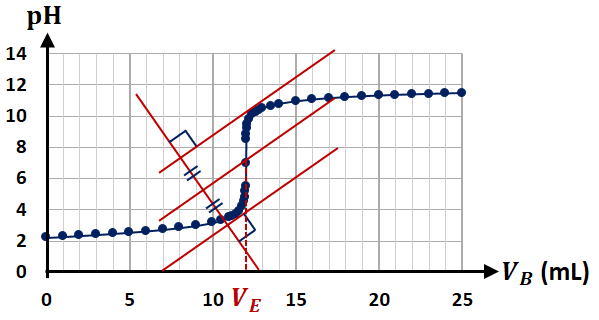
3) Titrage avec suivi pH-métrique
3.TP1 - Titrages directs pH-métriques
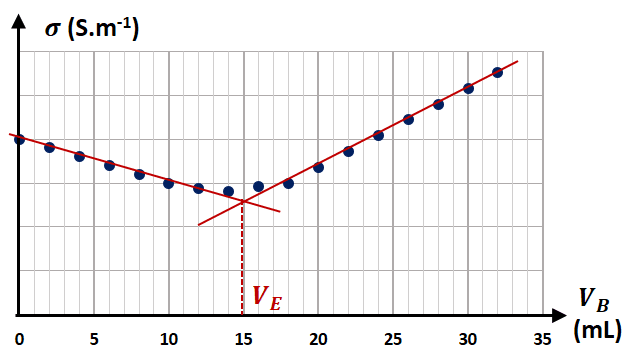
4) Titrage avec suivi conductimétrique
3.TP2 - Titrages directs conductimétriques