Incertitudes
I - Présentation des notions
1) Variabilité d’une mesure
Le but d’une mesure est d’attribuer une valeur numérique (avec son unité) à une grandeur.
Cependant, si la mesure est répétée plusieurs fois, le résultat ne sera pas exactement le même. On dit que la mesure d’une grandeur présente une variabilité
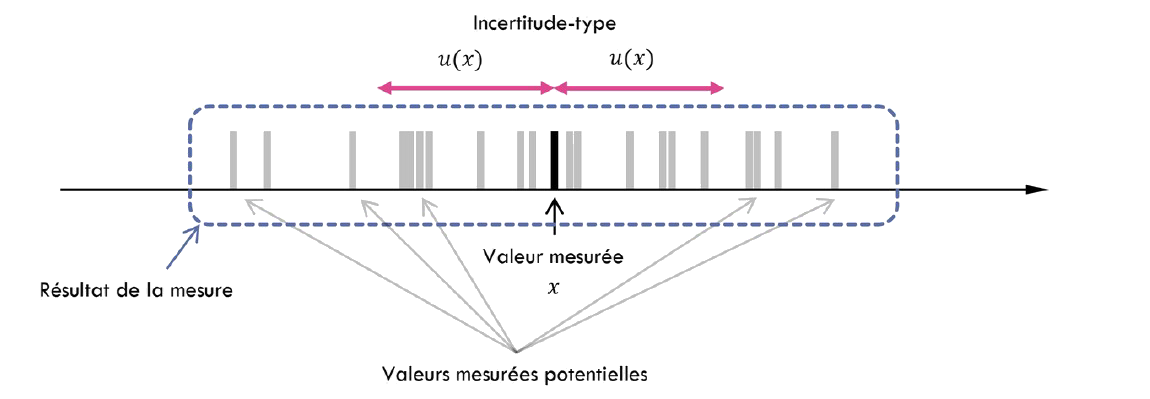
On va donc considérer qu’une mesure correspond en fait à un ensemble de valeurs mesurées (mesurées réellement ou potentiellement).
La variabilité d’une mesure dépend de nombreux facteurs :
- - le choix du protocole ;
- - la précision de l’appareil de mesure ;
- - l’habileté de la personne qui réalise les mesures ;
- - le contexte de la mesure…
2) Incertitude-type
L’« incertitude-type » est une estimation de l’étalement de l’ensemble des valeurs mesurées.
Si la grandeur mesurée est notée \(x\), l’incertitude-type est notée \(u(x)\). L'unité de l'incertitude-type \(u(x)\) est la même que celle de \(x\).
On utilise parfois l’incertitude-type relative définie par : \(\dfrac{u(x)}{x}\).
3) Écriture du résultat d’une mesure
Le résultat d’une mesure s’écrit :
- - soit sous la forme condensée : \(x ± u(x)\) ;
- - soit sous la forme séparée : \(x = …\) et \(u(x) = …\).
Important :
- Les incertitudes sont exprimées avec 1 chiffre significatif arrondi à la valeur supérieure.
- Le nombre de chiffres significatifs du résultat de la mesure doit être adapté en conséquence.
II - Détermination de l'incertitude-type
Pour cette partie, la démarche est à connaitre mais, au bac, les formules sont données dans les exercices.
1) Approche statistique (incertitude de type A)
L'incertitude de type A correspond à la situation où l'on dispose de plusieurs mesures de la même grandeur. Il est alors possible de procder àune analyse statistique.
• Le résultat de la mesure est la moyenne des valeurs mesurées. On le note en général \(\overline{x}\).
• L’incertitude-type pour la moyenne des valeurs mesurées est \(u(\overline{x}) = \dfrac{s_x}{\sqrt{N}}\) .
- où \(s_x\) est l’écart-type de l’ensemble des valeurs mesurées ;
- \(N\) est le nombre de valeurs mesurées.
• Utilisation de la calculatrice ou d’un tableur
La moyenne et l’écart-type se déterminent à l’aide des outils statistiques d’une calculatrice ou d’un tableur.
Suivant le modèle de calculatrice, l’écart-type à prendre en compte est noté « m », « xσn-1 », « Écart-type echantillon »…
2) Approche autre que statistique (incertitude de type B)
L'incertitude de type B correspond à la situation où l'on ne dispose que d'une mesure de la grandeur, mais où l'on connait le contexte de la mesure (appareil...).
• La démarche à adopter consiste à :
- - Rechercher les différentes causes d’incertitude ;
- - Évaluer les ordres de grandeur des différentes incertitudes et ne garder que les plus grandes ;
- - Combiner les incertitudes types : \(u(x) = \sqrt{(u_1(x))^2 + (u_2(x))^2 + ...}\)
• Exemples d'incertitudes-type suivant le type d'appareil utilisé pour faire la mesure :
| Type d'appareil | Information sur l'appareil | Exemples | Incertitude type |
|---|---|---|---|
| Appareils avec graduations | Graduation de valeur \(δ\) | Règle graduée en mm : \(δ = \pu{1 mm}\) | \(\dfrac{δ}{\sqrt{12}}\) |
| Appareils à affichage numérique | Quantification de valeur \(q\) | Balance à \(\pu{0,1 g}\) : \(q = \pu{0,1 g}\) | \(\dfrac{q}{2\sqrt{12}}\) |
| Appareils pour lesquelles la classe est précisée (verrerie) | Classe de valeur \(± a\) | Fiole jaugée : \(± \pu{0,06 mL}\) | \(\dfrac{a}{\sqrt{3}}\) |
3) Incertitude-type composée
La démarche qui suit est adaptée lorsqu’on cherche à évaluer l’incertitude-type d’une grandeur calculée à partir d’autres grandeurs pour lesquelles on connait les incertitudes-type.
• Avec un calcul du type \(C = A + B\), on peut montrer que \(u(C)= \sqrt{u(A)^2+u(B)^2 }\)
• Avec un calcul du type \(C = A × B\) ou \(C = \dfrac{A}{B}\), on peut montrer que \(\left(\dfrac{u(C)}{C}\right)^2 = \left(\dfrac{u(A)}{A}\right)^2 + \left(\dfrac{u(B)}{B}\right)^2\)
III - Validation du résultat : écart normalisé
Pour cette partie, la démarche et la formule sont à connaitre.
1) Écart normalisé entre une valeur mesurée et une valeur théorique
Par définition, l’écart-normalisé est : \(E_N = \dfrac{|m_{mes} - m_{réf} |}{u(m_{mes})}\)
2) Utilisation de l’écart normalisé
On peut considérer que la valeur mesurée est compatible avec la valeur de référence si \(E_N ≤ 2\).
Remarque : Plus \(E_N\) est petit, meilleur est le résultat.
